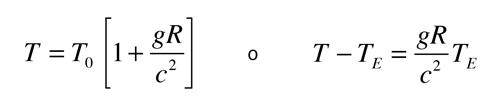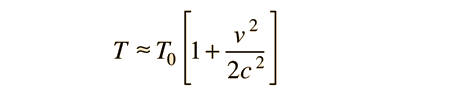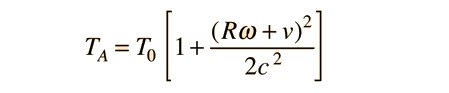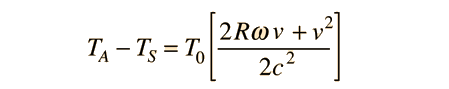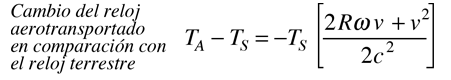Experimento de Hafele y Keating

"En octubre de 1971, cuatro relojes de haces atómicos de cesio, dieron dos veces la vuelta al mundo en vuelos regulares de aviones comerciales, una vez hacia el Este y otra vez hacia el Oeste, para probar la teoría de la relatividad de Einstein con relojes macroscópicos. Por las rutas de vuelo reales de cada viaje, la teoría predecía que los relojes en vuelo, en comparación con los relojes de referencia en el Observatorio Naval de los EE.UU., deberían perder 40+/-23 nanosegundos durante el viaje hacia el Este y ganar 275+/-21 nanosegundos durante el viaje hacia el Oeste... En relación con la escala de tiempo atómico del Observatorio Naval de los EE.UU., los relojes en vuelo perdieron 59+/-10 nanosegundos durante el viaje hacia el Este, y ganaron 273+/-7 nanosegundos durante el viaje hacia el Oeste, quedando los errores dentro de las desviaciones estándares correspondientes. Estos resultados proporcionan una clara resolución empírica de la famosa "paradoja" del reloj, con relojes macroscópicas".

J.C. Hafele and R. E. Keating, Science 177, 166 (1972)

Alrededor del Mundo

En 1971, experimentadores del Observatorio Naval de los EE.UU., realizaron un experimento para probar la dilatación del tiempo. Realizaron vuelos en líneas aéreas alrededor del mundo en ambas direcciones, donde cada circuito duraba unos tres dias. Llevaron consigo cuatro relojes atómicos de haces de cesio. Cuando regresaron y compararon sus relojes con el reloj del observatorio en Washington, D.C., habían ganado unos 0,15 microsegundos comparados con el reloj establecido en la tierra.

Relojes Atómicos Alrededor del Mundo

Desplazamiento de Tiempo Gravitacional

Para pequeños cambios en el campo gravitacional asociado con los cambios de altitud por encima de la tierra, la expresión de la dilatación del tiempo aproximada es

Si se hace una comparación entre un reloj en la superficie de la Tierra (T_E) y uno a una altura h por encima de la superficie (T), Hafele y Keating predijeron una diferencia de tiempo de 144 ns en un vuelo hacia el Este alrededor del mundo, en el que se invirtió un tiempo de vuelo de 41,2 horas. Esto se hizo a una altura promedio de vuelo razonable para una línea aérea comercial, de 8900 m. El desplazamiento de hora es positivo (envejecimiento más rápido), tanto en vuelo hacia el Este como hacia el Oeste. El valor esperado de 179 ns para el vuelo hacia el Oeste de 48,6 horas de duración, corresponde con una altitud media de unos 9400 metros.

Cálculo del Desplazamiento de Tiempo Cinemático

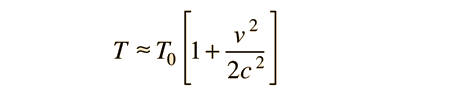
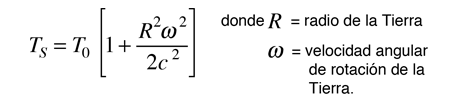
Esta expresión puede utilizarse para calcular la dilatación del tiempo en el experimento de Hafele-Keating en el cual, se tomó un reloj atómico a bordo de una aeronave y se comparó con un reloj situado en la tierra. El problema encontrado con la medición de la diferencia entre un reloj de superficie y uno en una aeronave, es que ninguna ubicación es realmente un marco inercial. Si se toma el centro de la Tierra como una aproximación a un sistema inercial, entonces se puede calcular la diferencia entre un reloj de superficie y el reloj de la aeronave. Tomando un "tiempo propio" en el centro de la tierra, como si el reloj maestro estuviera allí, el tiempo medido por un reloj en la superficie sería mayor

y eso para el reloj en el aire sería aproximadamente

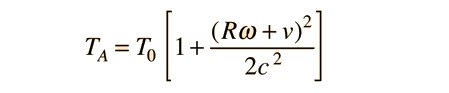
debido al nivel de las aproximaciones usadas, la altura de la aeronave no cambia significativamente el radio R. La diferencia en los tiempos en comparación con nuestro hipotético reloj maestro sería entonces

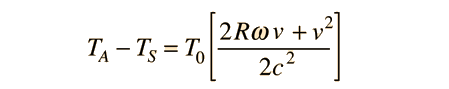
Ahora bien, esta relación es el inverso del experimento real, ya que se ha asumido que el reloj está en el centro de la tierra, mientras que los relojes reales están en los marcos que se están moviendo con respecto al centro. La expresión de diferencia de tiempo debe ser válida, pero al comparar el reloj del avión con el de la superficie, se debería encontrar que va por detrás, por tanto podemos modelar esa diferencia horaria por

Aplicación

Téngase en cuenta que en esta expresión, el tiempo del "centro de la tierra" ha sido sustituido por el tiempo en la superficie. En este caso esto es una aproximación válida, ya que la diferencia de tiempo es muchos órdenes de magnitud más pequeña que el propio tiempo, y esto nos permite modelar la diferencia entre dos tiempos mensurables.

Dilatación del Tiempo de la Aeronave

En un avión en vuelo sobre el ecuador, un reloj mostrará un desplazamiento de tiempo respecto de un reloj fijo en la superficie, que se puede modelar aproximadamente por la expresión

Mostrar

donde los subíndices A y S se refieren a los relojes del avión y la superficie. Para viajes hacia el Este, v tiene signo positivo y el desplazamiento será negativo (envejecimiento mas lento). Pero para un vuelo hacia el Oeste, el desplazamiento de tiempo es positivo (envejecimiento mas rápido), para las velocidades de vuelo implicadas. Hafele y Keating predijeron desplazamientos de tiempos de -184 ns para el vuelo hacia el Este alrededor del mundo, y un desplazamiento de +96 para el vuelo hacia el Oeste.

Si se especifican números para un vuelo en redondo de 48 horas a una velocidad constante sobre el ecuador, se obtienen -260 ns y 156 ns para los vuelos hacia el Este y Oeste respectivamente. Los valores predichos obtenidos por Hafele y Keating presumiblemente se basaron en mediciones detalladas de velocidades, etc.

A Hafele y Keating se les atribuye una medida experimental que confirma la dilatación del tiempo, y las predicciones coinciden con una precisión de aproximadamente 10%. Ellos dieron una respuesta experimental a la paradoja de los gemelos.