Medición de Eddington de la Deflexión de la Luz
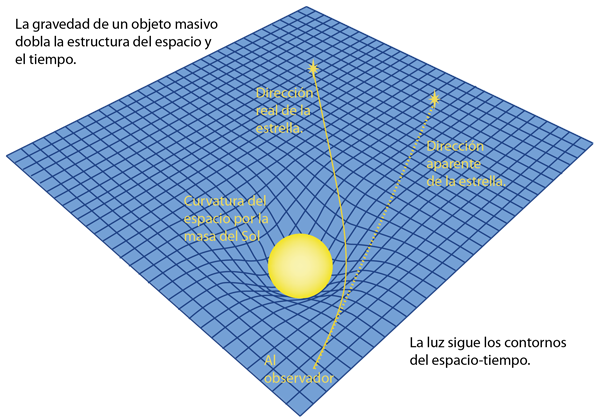
Los cálculos de Einstein en su recién desarrollada idea de la relatividad general indicaban que la luz de una estrella que apenas rozaba el sol debía ser desviada 1,75 segundos de arco. La representación de esta deflexión se ha exagerado enormemente en la ilustración anterior.
Einstein, escribiendo en una revista alemana durante la Primera Guerra Mundial, sugirió que durante un eclipse solar total, la deflexión debería ser observable en términos del tiempo de aparición de una estrella desde detrás del Sol. Fraknoi, et al. comentó que una copia de ese periódico llegó a la neutral Holanda y alcanzó al astrónomo británico Arthur S.Eddington. Se organizó una expedición para intentar medir esta deflexión durante el próximo eclipse solar total del 29 de mayo de 1919 en dos lugares: la isla de Principe de la costa oeste de África y Sobral, Brasil. Se obtuvieron fotografías en ambos lugares y se confirmó la deflexión pronosticada con una precisión de hasta un 20%.
Se han hecho varias veces mediciones durante eclipses solares totales, notablemente por el observatorio de Yerkes en 1953 y por la universidad de Tejas en 1973. Las mediciones de radiofrecuencia más exactas después de esos tiempos se han convertido en el acercamiento estándar a la deflexión gravitacional de las ondas electromagnéticas.
|
Índice
Ideas de Relatividad General
Fraknoi, Morrison, Wolff
Cap. 23 |


