Alcance Relativista
La capacidad de detectar una partícula de corta duración, depende de si tiene el suficiente alcance dentro del acelerador, para llegar al detector. Este es un problema serio con partículas que pueden tener un tiempo de vida media tan corto como ¡10-16 segundos! Incluso viajando a la velocidad de la luz, solo recorrerá en promedio, 0,03 micrómetros antes de decaer. La detección práctica de partículas de corta vida, depende de la dilatación de tiempo relativista.
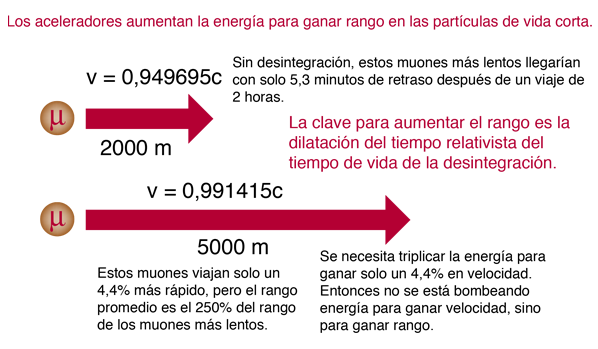
Debido a que los relojes de las partículas a alta velocidad funcionan más lentamente que en el marco del laboratorio, las partículas tienen un alcance más largo en el acelerador del que podría anticiparse con un tratamiento no relativista. Los números en la ilustración anterior se puede verificar en el cálculo siguiente.
Nota: Por defecto se usan los parámetros del muón. Se pueden cambiar todos los valores.
Un ejemplo que requiere el alcance relativista para explicar los datos observados, se da en el flujo del muón en la superficie de la Tierra.
| Cantidades Mecánicas Relativistas |
| Una Visión General del Tiempo |
| HyperPhysics*****Relatividad | M Olmo R Nave |