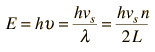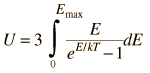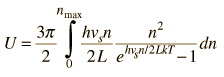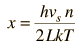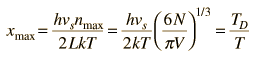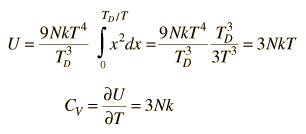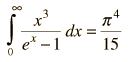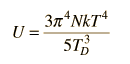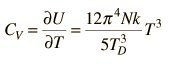¿Que es un Fonón?

Al considerar una celosía regular de átomos en un material sólido uniforme, se podría esperar que hay una energía asociada con las vibraciones de estos átomos. Pero estos átomos están atados entre sí por medio de enlaces, de modo que no pueden vibrar independientemente. Las vibraciones por tanto toman la forma de modos colectivos, que se propagan a través del material. Tales vibraciones de la red de propagación pueden ser consideradas como ondas de sonido, y su velocidad de propagación es la velocidad del sonido en el material.

Las energías vibracionales de las moléculas, por ejemplo, una molécula diatómica, se cuantifican y se tratan como osciladores armónicos cuánticos. Los osciladores armónicos cuánticos tienen niveles de energía igualmente espaciados, con una separación DE = hu. Así que los osciladores puede aceptar o perder energía sólo en unidades discretas de energía hu.

La evidencia sobre el comportamiento de la energía vibracional en sólidos periódicos está en que, los modos de vibración colectiva pueden aceptar energía sólo en cantidades discretas, y estos cuantos de energía han sido etiquetados como "fonones". Al igual que los fotones de energía electromagnética, obedecen a las estadísticas de Bose-Einstein.

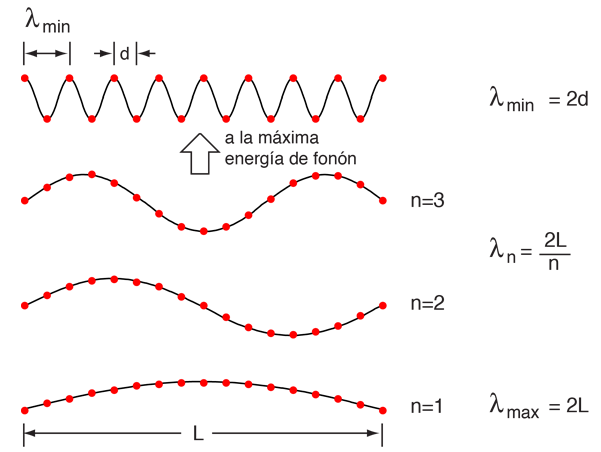
Considerando un sólido como una matriz periódica de puntos de masa, hay limitaciones tanto en el mínimo como en el máximo de longitud de onda asociado con un modo vibracional.

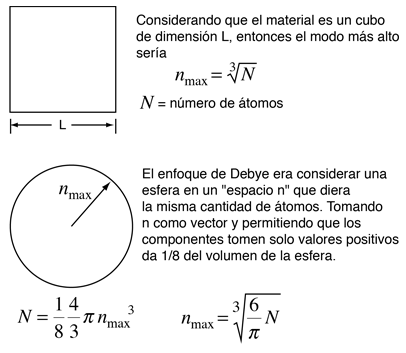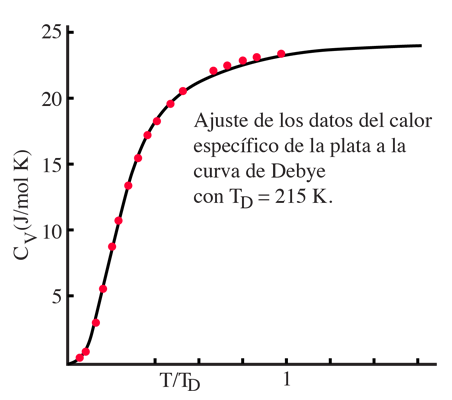
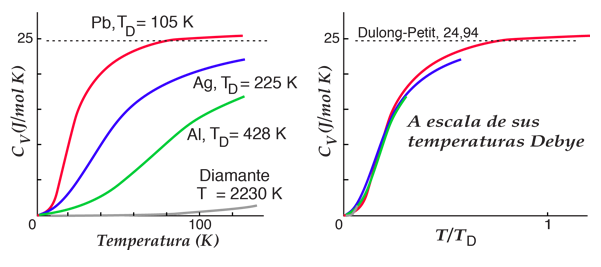
Asociando la energía del fonón 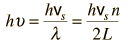con los modos y sumando los modos, Debye fue capaz de encontrar una expresión de la energía como una función de la temperatura y derivar una expresión para el calor específico del sólido. En esta expresión, vs es la velocidad del sonido en el sólido.

Calor Específico Debye

Asociando la energía del fonón con los modos vibracionales del sólido

donde v_s es la velocidad del sonido en el sólido, Debye abordó la materia del calor específico en los sólidos. Tratándolos con las estadísticas de Einstein-Bose, la energía total de las vibraciones de la red es de la forma

Esto se puede expresar en términos de modos de fonón, expresando la integral en términos del número de modos n.

Aquí el factor 3p/2 viene de tres consideraciones. Primera, hay 3 modos asociados con cada número de modo n: un modo longitudinal y dos modos transversales. Luego se obtiene un factor de 4p² por integración sobre las coordenadas angulares, tratando el número de modo n como el radio-vector. Finalmente se limita la integral al cuadrante en el cual, todas las componentes de n son positivas, dando un factor de 1/8: el producto de estos es 3p/2.

Para resolver la integral, se realiza la sustitución

y el límite de la integral en términos de x se obtiene de

Donde se introduce aquí la constante T_D. Se le llama temperatura Debye y es una constante asociada con el modo vibracional mas alto permitido.

Cuando se ponen todas las constantes, la integral toma la forma

La expresión del calor específico Debye es la derivada de esta expresión con respecto a T. La integral no se puede evaluar en forma cerrada, pero la evaluación numérica muestra un resultado razonablemente de acuerdo con los calores específicos de los sólidos observados para todo el rango de temperatura, alcanzando la ley de Dulong-Petit a altas temperaturas y el comportamiento característico T³ a muy bajas temperaturas.

La expresión del calor específico que surge de la teoría de Debye, se puede obtener tomando la derivada de la expresión de la energía de arriba.

Esta expresión se puede evaluar numericamente para una determinada temperatura por medio de una rutina de ordenador.

Los datos para la plata que se muestra a la izquierda es de Meyers. Muestra que el calor específico coincide con el modelo de Debye a ambas temperaturas alta y baja.

Como la expresión del calor específico de Debye, se puede evaluar como una función de la temperatura y da una curva teórica que tiene una forma específica como función de T/T_D, los calores específicos de diferentes sustancias se pueden solapar si se dibujan en función de este ratio. Abajo a la izquierda se trazan los calores específicos de cuatro sustancias como función de la temperatura y se muestran muy diferentes. Pero si se escalan a T/T_D, aparecen muy similar y muy próximos a la teoría de Debye.

Límites a Alta y Baja Temperatura
Calor Específico Debye

La expresión de la energía de la teoría de Debye del calor específico, es de la forma

donde TD = Temperatura Debye.

Aunque esta integral no puede evaluarse en forma cerrada, si se pueden obtener los límites a alta y baja temperatura.

En el caso de alta temperatura donde T>>T_D, el valor de x es muy pequeño en el rango de la integral. Esto justifica el uso de la aproximación de exponencial de las series exponenciales, e^x = 1 + x. Esto reduce la expresión de la energía a

que es el resultado de Dulong-Petit de la termodinámica clásica.

Para bajas temperaturas donde T<< T_D, el exponencial en el denominador se hace muy grande antes de alcanzar el límite, implicando con ello que el integrando es muy pequeño cerca del límite superior. Esto hace plausible aproximar la integral por medio de incrementar el límite a infinito para hacer uso de la integral estandar.

Luego la energía es entonces

y el calor específico es

Esta dependencia de T³ del calor específico a muy baja temperatura, esta de acuerdo con los experimentos con los no metales. En los metales, el calor específico del electrón se hace significativo a bajas temperaturas y se combina con el calor específico de red de arriba en el calor específico de Einstein-Debye.