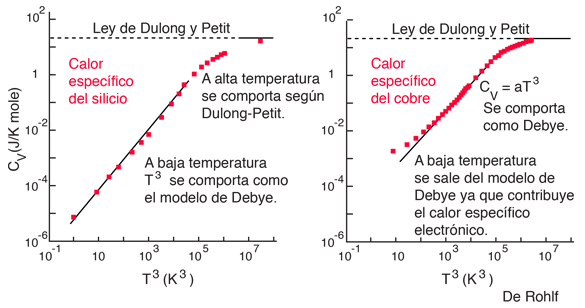
Contribución de Debye a la Teoría del Calor Específico La aplicación del oscilador de Einstein al calor específico, le proporcionó al experimento una concordancia cualitativa, y le dió el correcto límite a alta temperatura (la ley de Dulong y Petit). El ajuste cuantitativo del experimento, se mejoró con el reconocimiento de Debye de que había un número máximo de modos de vibración en un sólido. Se imaginó a las vibraciones en forma de modos de ondas estacionarias en el cristal, similar a los modos electromagnéticos en una cavidad, que se explica con éxito en la radiación del cuerpo negro. La densidad de estados de estos modos, que se llaman "fonones", es de la misma forma que la densidad de estados de fotones en una cavidad. Para imponer un límite finito al número de modos en el sólido, Debye utilizó un máximo de frecuencias de fonones permitida, que ahora se llama frecuencia de Debye υD. 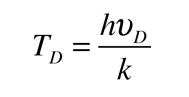En el tratamiento del calor específico, se define la temperatura de Debye por Para bajas temperaturas, la aportación de Debye condujo a un calor específico 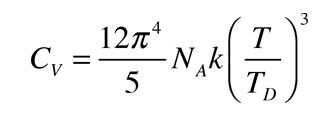Mostrar La dependencia del cubo de la temperatura, está de acuerdo con los resultados experimentales de los no metales, y de los metales cuando se toma en consideración el calor específico del electrón. Las medidas de la variaciones del calor específico con la temperatura a bajas temperaturas, ha llevado a la tabulación de las temperaturas Debye de un número de materiales sólidos. La expresión completa del calor específico Debye se debe evaluar por procedimientos numéricos. Tiene los correctos valores límites a ambas temperaturas alta y baja. Definición de Constantes Tabla de Calores Específicos Expresión del Calor Específico de Einstein-Debye Tabla de Temperaturas de Debye

Índice Referencia Rohlf Cap. 14. Blatt Sec. 4.3

HyperPhysics*****Termodinámica M Olmo R Nave

Atrás

Calores Específicos de Einstein-Debye En la variación del calor específico respecto de la temperatura, el modelo de fonón de Einstein-Debye produjo concordancia con la dependencia del cubo de la temperatura para valores bajos. La contribución principal de los modelos de Einstein y Debye, fue la explicación de las drásticas desviaciones de la ley de Dulong y Petit. El paso final en la explicación del calor específicos a baja temperatura de los metales, fué la inclusión de la contribución del electrón al calor específico. Cuando se combinaron todos ellos se produjo la expresión Fíjese que la parte vibracional solamente, es el límite a temperatura baja del mas general calor específico de Debye. Los datos de abajo, muestran que el modelo de fonón de Debye con su dependencia cúbica de la temperatura, coincide en los datos del silicio a muy bajas temperaturas. El cobre muestra una diferencia con la dependencia cúbica, mostrando la evidencia del calor específico del electrón. Aquí el término vibracional, es solo el límite a baja temperatura de la expresión del calor específico de Debye; la expresión completa incluye una integral que se debe evaluar numéricamente. Produce una buena concordancia con la transición al límite de Dulong y Petital altas temperaturas. Note que el modelo de calor específico presentado aquí, usa ambas fórmulas de la estadística cuántica. La estadística de Bose-Einstein se usa para describir la contribución por las vibraciones de las redes (fonones), y la estadística de Fermi-Dirac se debe usar para describir la contribución del electrón al calor específico.

Índice Referencias Blatt Sec 4.3. Rohlf Cap. 14.

HyperPhysics*****Termodinámica M Olmo R Nave

Atrás