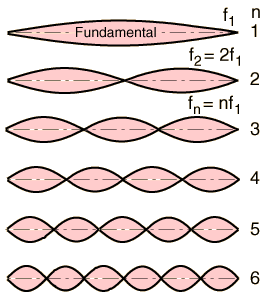
Vibración de una Cuerda
El modo de vibración fundamental de una cuerda estirada es tal que, la longitud de onda es dos veces la longitud de la cuerda.
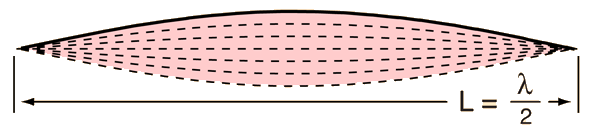
Aplicando las relaciones de onda básicas, da la expresión para la frecuencia fundamental:
 | Calcular |
| Puesto que la velocidad de onda está dada por | 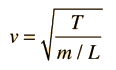 | , la expresión de frecuencia |
se puede poner en la forma:
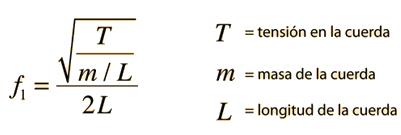
La cuerda también vibrará en todos los armónicos de la fundamental. Cada uno de estos armónicos, formará una onda estacionaria en la cuerda.

Esto muestra una onda estacionaria resonante en una cuerda. Está impulsada por un vibrador a 120 Hz.

En las cuerdas de rigidez finita, las frecuencias armónicas se desviarán progresivamente de los armónicos matemáticos. Para obtener la masa necesaria en las cuerdas de bajos eléctricos como se muestra arriba, el alambre se enrolla alrededor de otro alambre de núcleo sólido. Esto permite la adición de masa sin producir una rigidez excesiva.
| Mediciones de Ejemplos en una Cuerda de Acero |
| Frecuencias de Cuerdas | Instrumentos de Cuerda | Ilustración con un Slinky | Forma Matemática |
Conceptos de Movimiento Periódico
Conceptos de Resonancia
| HyperPhysics*****Sonido | M Olmo R Nave |

 T = tensión en la cuerda
T = tensión en la cuerda