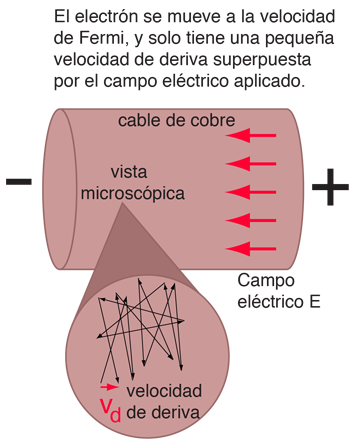
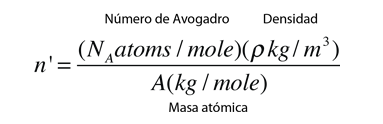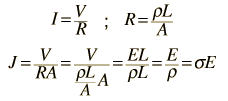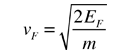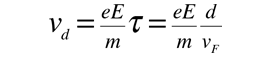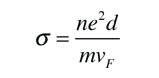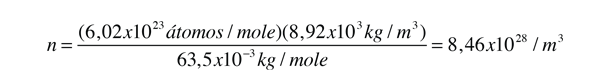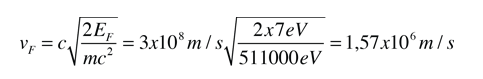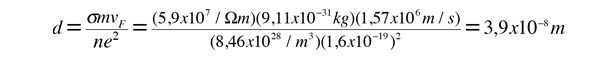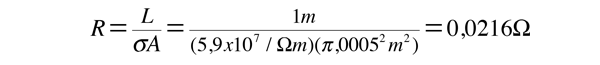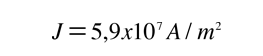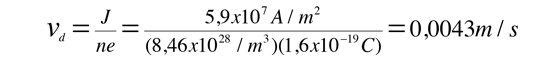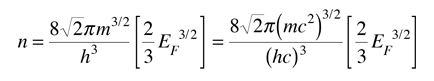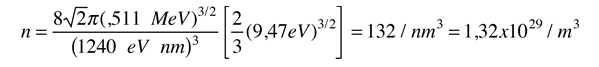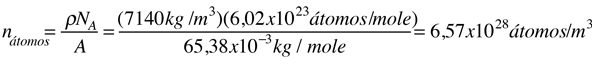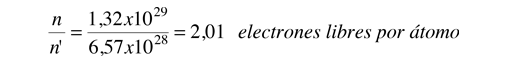Vista Microscópica del Conductor de Cobre
Como ejemplo de la vista microscópica de la ley de Ohm, se va a examinar los parámetros para el cobre. Con un electrón libre por átomo en su estado metálico, la densidad de electrones para el cobre se puede calcular de su densidad de materia y su masa atómica.
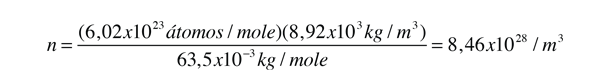
La energía Fermi para el cobre es de unos 7 eV., de modo que la velocidad de Fermi es
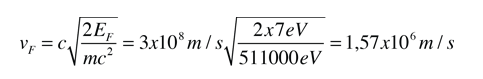
La densidad del cobre medida a 20°C is

El camino libre medio de un electrón bajo estas condiciones, se puede calcular de
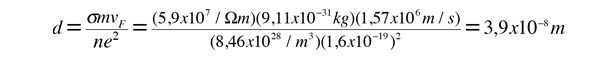
La velocidad de desplazamiento depende del campo eléctrico aplicado. Por ejemplo, un hilo de cobre de 1 mm. de diámetro y un metro de longitud, al que se tiene aplicado 1 voltio, nos lleva a los siguientes resultados.
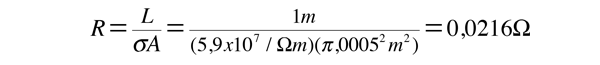
Para un voltio aplicado, da una intensidad de 46.3 Amperios y una densidad de corriente
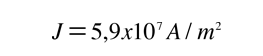
Esto corresponde a una velocidad de desplazamiento de solamente milímetros por segundo, en contraste con la alta velocidad de Fermi para los lectrones.
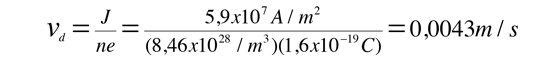
¡Peligro! ¡No intente esto en el hogar! El Dr. Beihai Ma de Argonne National Laboratory, escribió para señalar que la densidad de corriente de 5.900 A/cm2 de este ejemplo, es unas diez veces la densidad de corriente de 500 A/cm2 que normalmente puede soportar el cobre a 40°F. Así que hacer esto en el laboratorio puede ser muy emocionante. Gracias por las comprobaciones al Dr. Ma.
(Si reducimos el voltaje aplicado de manera que la corriente sea exactamente 3 Amperios, la densidad de corriente será de 382 A/cm2, de modo que el hilo de cobre permanecerá intacto y la velocidad de desplazamiento calculada es exactamente 0.00028 m/s. Estos datos son mas típicos para estas condiciones de trabajo.)
¿Qué Ocurre con los Efectos Cuánticos y las
Estadísticas de Fermi-Dirac?
El tratamiento microscópico de la Ley de Ohm y la velocidad de deriva
anterior es básicamente un tratamiento clásico. Pero sabemos que los
electrones en un metal obedecen las estadísticas de Fermi-Dirac, y que a
bajas temperaturas, todos los niveles de energía de electrones disponibles
se llenan hasta el Nivel de Fermi .
También sabemos que este nivel de Fermi (aproximadamente 7 eV en el cobre)
es muy alto en comparación con la
energía térmica a temperatura ambiente .
Entonces, ¿cómo justificamos usar toda la población de electrones libres
anterior en el cálculo de la velocidad de deriva cuando para las
interacciones térmicas, solo los electrones dentro de aproximadamente kT del
nivel de Fermi son accesibles a la interacción?
Un lugar donde se discute esta situación es en el clásico libro de
Física del Estado Sólido de Charles Kittel. Señala que debido a la población
completa de electrones de conducción hasta el nivel de Fermi, estos
electrones en el cable de cobre tienen una velocidad muy alta, del orden de
1,6 x 10 6 cm/seg para el cobre. Un campo eléctrico aplicado
externamente en un cable de cobre ejercerá una fuerza continua sobre los
electrones y continuaría acelerándolos si esa aceleración no fuera
aleatorizada por las colisiones mltiples y la interacción con la red.
La observación de la Ley de Ohm nos muestra experimentalmente que se logra
una corriente de equilibrio, y que la presunción de que todos los electrones
de conducción están participando, nos permite proyectar una velocidad de
deriva efectiva para estos electrones bajo la influencia del campo eléctrico
aplicado. Se observa que esta es una presunción completamente clásica.
Mientras Kittel examina más a fondo la conductividad eléctrica desde el
punto de vista de las estadísticas de Fermi-Dirac, hace el siguiente
comentario: "Es un hecho algo sorprendente que la introducción de la
distribución de Fermi-Dirac en lugar de la distribución clásica
Maxwell-Boltzmann, generalmente tiene poca influencia en la conductividad
eléctrica, a menudo solo cambia el tipo de promedio utilizado en la
especificación del tiempo de relajación. A primera vista, se podría haber
esperado encontrar un cambio más drástico porque con la distribución de
Fermi-Dirac solo pueden participar en procesos de colisión aquellos
electrones cerca la superficie de Fermi".
Kittel argumenta que el principio de exclusión no previene la
intervención del campo eléctrico, ya que acta sobre cada electrón en la
distribución para producir el mismo cambio de velocidad. Siempre hay un
estado vacante listo para recibir el electrón que está cambiando su estado
bajo la acción del campo eléctrico, produciéndose la vacante por el cambio
simultáneo del estado de otro electrón. En contraste con un proceso de
colisión térmica aleatorio, la fuerza eléctrica de dirección nica produce
estados de exceso de electrones A y estados de deficiencia de electrones B
que permiten las colisiones específicas requeridas para restablecer el
equilibrio. El principio de exclusión previene muchas colisiones, pero
permite las colisiones necesarias para restablecer el equilibrio. La
conclusión es que, a excepción de la naturaleza detallada del tiempo de
relajación, la situación es esencialmente la misma que en la situación
clásica, y conduce a la misma expresión de conductividad y velocidad de
deriva promedio.
|