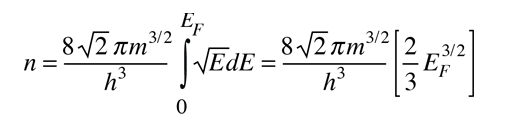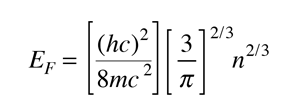Olas en el Mar de Fermi
La energía Fermi es la máxima energía ocupada por un electrón a 0ºK. Por el principio de exclusión de Pauli, se sabe que los electrones llenarán todos los niveles de energías disponibles, y el tope de ese "líquido de Fermi" de electrones se llama energía Fermi o nivel de Fermi. Una de las cosas destacables sobre la energía Fermi es su tamaño, en comparación con las energías que podrían ganar los electrones en las interacciones físicas ordinarias con su entorno.
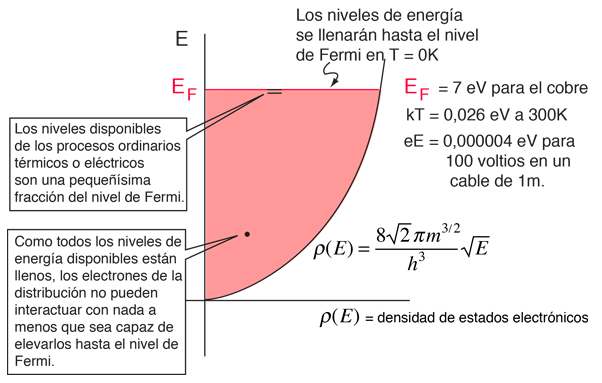
La cantidad de energía disponible como resultado de la temperatura del material es del orden de la energía térmica media, siendo una relación representativa kT= 0,026 eV a 300ºK. Esta es muy pequeña en comparación con la energía de Fermi de 7 eV para el cobre. Esto dice que la energía térmica puede interactuar con sólo una pequeña fracción de los electrones (aproximadamente 0,026/7, o aproximadamente el 0,4% del rango de energía), ya que la inmensa mayoría de los electrones estan separados de la parte superior del mar de Fermi por mucho más que la energía térmica. Esto se correlaciona bien con la observación de que los electrones no contribuyen significativamente al calor específico de los sólidos a temperaturas ordinarias. Sólo a temperaturas muy bajas el calor específico de electrones viene a ser significativo.
Puesto que hay un vasto mar de electrones, puede ser más fácil visualizar la falta de disponibilidad de los estados finales con un sistema más simple que la de los electrones atómicos, que debe obedecer el principio de exclusión de Pauli. Abajo a la izquierda en el ejemplo de un átomo de cloro, la energía podría ser recibida de fotones que coincidan con la diferencia de energía entre n = 1 y n = 2, porque hay una vacante de energía en el nivel n = 2. Pero para el neón, incluso un fotón que tenga precisamente la energía E2-E1 no puede ser absorbida debido a que están llenos todos los niveles disponibles.

La gran mayoría de los electrones libres están igualmente indisponibles para el proceso de conducción eléctrica ordinaria en los cables, para el mismo tipo de razones. Cuando se aplica un voltaje a un conductor de cobre, se establece un campo eléctrico en el cable, que puede hacer trabajo sobre los electrones para darles energía. Pero el ejemplo de la conducción por cable de cobre, muestra que el camino libre medio de los electrones en un cable de cobre a la temperatura ambiente, está en la vecindad de 40 nm. Así la energía dada a un electrón por el campo eléctrico de 100 voltios aplicado a un hilo de cobre de 1 metro, sería del orden de W=eEd = 100 voltios x 40 nm = 0,000004 eV. Tal cantidad de energía no puede ser absorbido por la mayoría de los electrones porque no hay nivel de energía disponible que se acerque en esa cantidad de energía.
|
Índice
Conceptos de Semiconductor
Semiconductores en Electrónica
Referencia
Rohlf
Sec 14-2 |