Colisiones en Dos Dimensiones
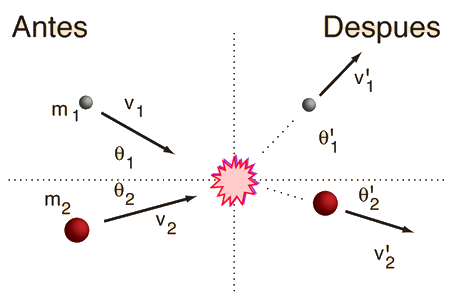
En el caso general de una colisión en dos dimensiones entre dos masas, no se puede prever la cantidad de energía cinética que se pierde en la colisión. Por lo tanto, las velocidades de las dos masas después del choque, no están completamente determinadas por sus velocidades y direcciones antes de la colisión. Sin embargo, la conservación del momento se debe satisfacer, de modo que si se especifica la velocidad de una de las partículas después de la colisión, la otra se podrá determinar.
Puesto que el momento se debe conservar tanto en magnitud como en dirección, se debe encontrar el vector del momento inicial. Esto se hace expresando el momento en sus componentes, usando la notación del vector unitario. Luego son combinadas las componentes, para dar el momento total del sistema antes de la colisión.
Entre valores para las masas y velocidades arriba. Luego especifique una velocidad final abajo.
Si del cálculo resulta ángulos positivos, significan que han resultado en el sentido mostrados en el diagrama. Si los ángulos son negativos, eso significa que los ángulos giran a la dirección opuesta del eje x, de la indicada en el diagrama.
Para los objetos ordinarios, la energía cinética final será menor que el valor inicial. La única manera que usted puede conseguir un aumento de energía cinética es, si hay algún tipo de liberación de energía provocada por el impacto. ¿Era una granada de mano uno de los objetos?
|
Indice
Conceptos sobre Colisión
Colisiones Elásticas
Colisiones Elásticas Frontales |