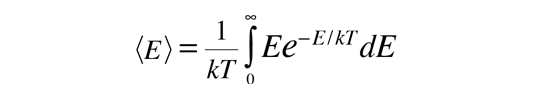Energía Cinética Molecular Media

Las moléculas de la materia a temperaturas normales, se pueden considerar que estan en un incesante movimiento aleatorio a gran velocidad. De la distribución de Boltzmann, se puede deducir el promedio de la energía cinética de traslación de estas moléculas. Cuando la distribución de Boltzmann

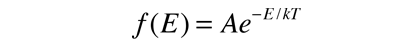
se aplica al movimiento de una molécula en una dimensión, esto se convierte en

Mostrar

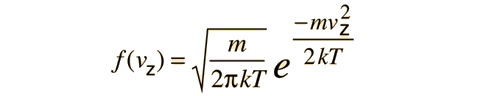Se puede usar esta función de distribución, para calcular el valor medio del cuadrado de la velocidad.

Esta integral se puede poner en la forma estándar:

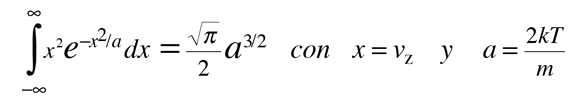
esto da:

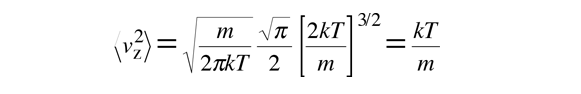
La energía cinética media en una dimensión, es entonces

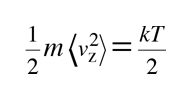
y en las tres dimensiones de ese movimiento, la energía cinética media es:

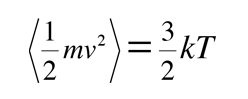
Podemos con confianza multiplicar el resultado de una dimensión por tres, ya que los diferentes componentes de la velocidad son independientes el uno del otro. Esta asignación de kT/2 de la energía para cada grado de libertad de movimiento de la molécula, se llama equipartición de la energía. Esta energía cinética microscópica es a menudo llamado "energía térmica", y esta expresión es útil para definir la temperatura cinética.

Tenga en cuenta que la energía cinética media de las moléculas, no es lo mismo que la energía media de las energías puramente aleatorias en la distribución de Boltzmann, que es E_avg= kT. Si se tiene en cuenta que todas las velocidades son igualmente probables, entonces puede considerarse que todas las velocidades dentro de un rango de v a v+Δv, forman una cáscara esférica en el "espacio de velocidades". Para un mayor valor de v, la cáscara es más grande y hay más posibilidades. Esto revierte a que la energía cinética media tome un valor más alto, que resulta ser 3kT/2 en lugar de kT. Este tipo de consideración surge en el desarrollo de la distribución de velocidades de Maxwell para las moléculas.

Integral de Energía Media: Distribución de Boltzmann

La integral de energía media para la distribución de energías entre una colección de partículas de acuerdo con la distribución de Boltzmann es:

Se puede evaluar esta integral, utilizando la integración por partes.

Esta técnica es particularmente apropiada para eliminar un término lineal que está multiplicando en un exponente.