La Molécula de Hidrógeno

La molécula de hidrógeno, el caso clásico del enlace covalente, se forma por la superposición de las funciones de onda de los respectivos electrones de los átomos de hidrógeno, en una interacción que se caracteriza como interacción de intercambio. El carácter de este enlace es completamente diferente del enlace iónico que se forma en el cloruro de sodio, NaCl. Si se mide entonces el balance de energía cuando se forman los iones H+ y H-, y se examina la fuerza de atracción entre ellos, la energía que se requiere es positiva para cualquier valor de separación de iones. Es decir, no existe una distancia en la que haya una interacción de atracción neta, por lo que el enlace no puede ser iónico.

La distribución de los electrones alrededor de los protones del hidrógeno se describe por una función de onda mecánica cuántica, y la función de onda que describe los dos electrones de un par de átomos puede ser simétrica o antisimétrica con respecto al intercambio de electrones idénticos. Por el principio de exclusión de Pauli, se sabe que las funciones de onda de dos fermiones idénticos deben ser antisimétricas. La parte de la función de onda del espín del electrón puede ser simétrica (espines paralelos) o antisimétrica (espines opuestos), pero entonces la parte espacial de la función de onda debe ser opuesta. Eso garantiza que la función de onda completa (el producto de las funciones de onda de espín y de espacio) es antisimétrica. A continuación se muestran las dos posibilidades para las funciones de onda espaciales para hidrógenos distantes.

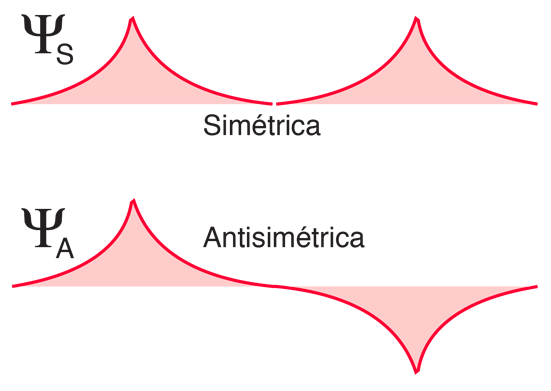
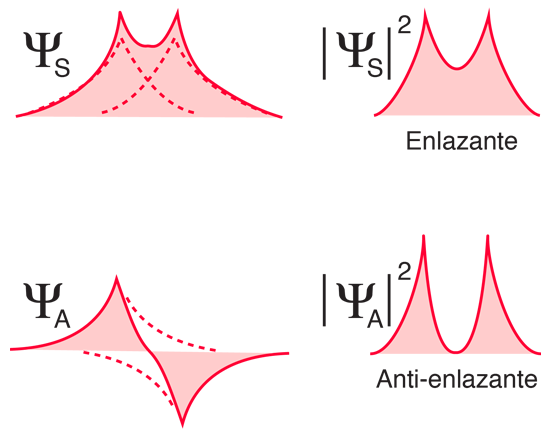
Como se muestra abajo, cuando se juntan los átomos de hidrógeno, la función de onda espacial simétrica conduce a una configuración de enlace de los electrones, y la antisimétrica no lo hace. La densidad de carga electrónica real viene dada por el cuadrado de la magnitud de la función de onda, y se puede ver que la función de onda simétrica da una alta densidad electrónica entre los núcleos, lo que conduce a una fuerza neta de atracción entre los átomos (un enlace).

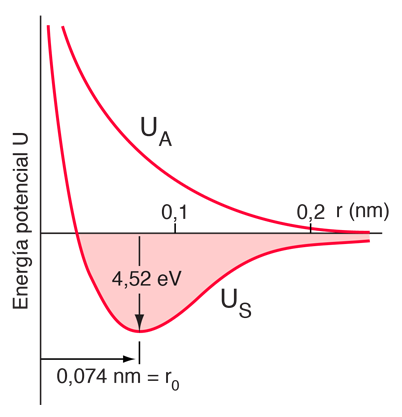La interacción de intercambio (que es un efecto mecánico cuántico completamente) conduce a un enlace fuerte de la molécula de hidrógeno, con una energía de disociación de 4,52 eV a una separación de 0,074 nm. La energía potencial del orbital anti-enlazante da una idea de por qué un tercer átomo de hidrógeno no se puede unir a los dos átomos de la molécula de hidrógeno. Sería en una situación anti-enlazante con uno de los otros átomos de hidrógeno y por lo tanto sería repelido. Se dice que el enlace en la molécula de hidrógeno está "saturado" porque no puede aceptar otra unión mas.