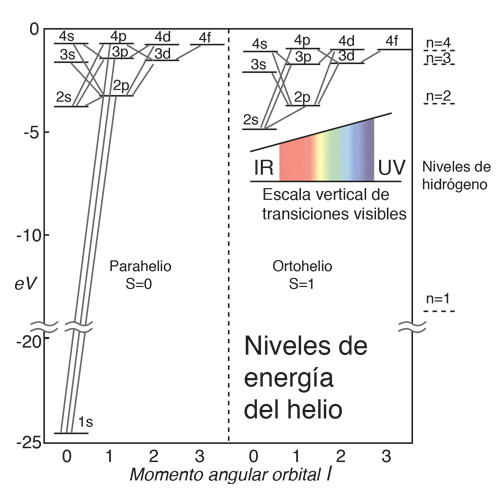
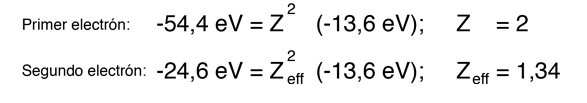Niveles de Energía del Helio

Los niveles de energía de los electrones de un átomo de helio, demuestran una serie de características de los átomos multielectrónicos.

Un electrón se presume que está en el estado fundamental, el estado 1s. Un electrón en un estado superior puede tener espín antiparalelo al electrón del estado fundamental (S = 0, estado de singlete, parahelio) o paralelo al electrón del estado fundamental (S = 1, estado de triplete, ortohelio).

¿Por qué son más Bajos los Estados Ortohelio? Comentarios sobre los Niveles de Energía del Helio

Niveles de Energía en Parahelio y Ortohelio

En el diagrama de niveles de energía, un electrón se presume que está en el estado fundamental, el estado 1s. Un electrón en un estado superior, puede tener espín antiparalelo al electrón del estado fundamental (S = 0, estado de singlete, parahelio), o paralelo al electrón del estado fundamental (S = 1, estado de triplete, ortohelio).

Se observa que los estados ortohelios están a un nivel mas bajo de energía que los estados parahelios. La explicación para esto es:

1. Los espines paralelos hacen que sea simétrica la parte del espín de la función de onda.
2. La función de onda total de los electrones debe ser anti-simétrica, ya que son fermiones y deben obedecer el principio de exclusión de Pauli.
3. Esto obliga a la parte del espacio de la función de onda, a ser anti-simétrica. La función de onda de los electrones, se puede escribir como el producto de la parte espacial y de espín, de la función de onda.
4. Una función de onda de espacio anti-simétrica para los dos electrones, implica una mayor distancia promedio entre ellos, que una función simétrica del mismo tipo. La probabilidad es el cuadrado de la función de onda, y desde un simple punto de vista funcional, el cuadrado de una función antisimétrica, debe ir a cero en el origen. Así, en general, la probabilidad de pequeñas separaciones de los dos electrones, es menor que para una función de onda de espacio, simétrica.
5. Si los electrones tienen una separación promedio, entonces habrá menos protección del núcleo por el electrón del estado fundamental, y el electrón del estado excitado estará por lo tanto más expuesto al núcleo. Esto implica que estará más fuertemente unido y con menor energía.

Este efecto se llama a veces la "interacción espín-espín", y está dirigida por la Regla de Hund #1. Forma parte de la comprensión del ordenamiento de los niveles de energía en los átomos multi-electrónicos.

Niveles de Energía del Helio

El estado fundamental del helio tiene dos electrones idénticos 1s. La energía requerida para extraer uno de ellos, es la energía de ionización más alta de cualquier átomo en la tabla periódica: 24,6 electronvoltios. La energía necesaria para extraer el segundo electrón es 54,4 eV, como sería de esperar, según el modelado de los niveles de energía del hidrógeno. El ión He+, es justo como un átomo de hidrógeno, con dos unidades de carga en el núcleo. Dado que los niveles de energía del hidrógeno dependen del cuadrado de la carga nuclear, la energía del electrón restante del helio, debe ser justo 4x(-13,6 eV) = -54,4 eV., como se observó.

El hecho de que el segundo electrón esté unido con menos fuerza, se puede interpretar como un efecto del blindaje; el otro electrón blinda parcialmente el segundo electrón, de la carga completa del núcleo. Su energía puede ser utilizada, para modelar el blindaje eficaz de la siguiente manera.

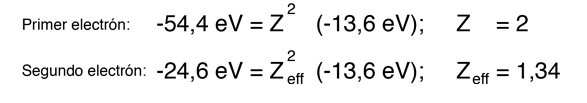
Otra forma de ver la energía es, decir que la repulsión de los electrones contribuye a la energía potencial positiva, que compensa parcialmente la energía potencial negativa, presentada por la fuerza de atracción eléctrica de la carga nuclear. La descripción de cualquier electrón en un átomo multi-electrónico, debe encontrar una manera de caracterizar el efecto de los otros electrones sobre la energía.