Energía Cinética Rotacional

La energía cinética de un objeto girando es análoga a la energía cinética lineal y puede expresarse en téminos del momento de inercia y de la velocidad angular. La energía cinética total de un objeto extenso, se puede expresar como la suma de la energía cinética de traslación de su centro de masa y la energía cinética de rotación sobre el centro de masa. Para un eje de rotación fijo dado, la energía cinética, se puede expresar en la forma

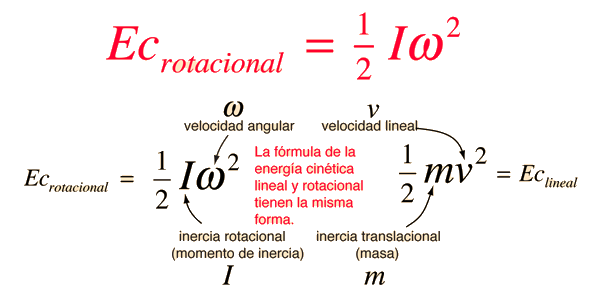
Las expresiones para la energía cinética rotacional y lineal puede desarrollarse en paralelo desde el principio de trabajo-energía. Considera el siguiente paralelismo entre un par constante ejercido sobre un volante con momento de inercia I, y una fuerza constante ejercida sobre una masa m, ambas empezando desde el reposo.

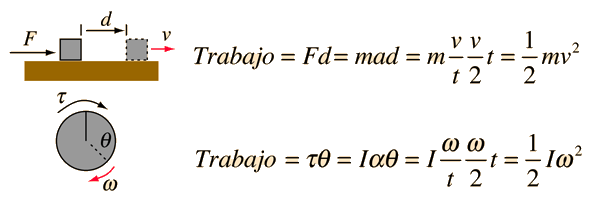
Para el caso lineal, empezando desde el reposo, la aceleración por definición es igual a la velocidad final dividida por el tiempo y la velocidad media es la mitad de la velocidad final, mostrando que el trabajo realizado por el bloque es igual a la energía cinética. Para el caso rotacional, también empezando desde el reposo el trabajo rotacional es τθ y la aceleración angular α dada al volante, se obtiene de la segunda ley de Newton para la rotación. La aceleración angular es igual a la velocidad angular final dividido por el tiempo y la velocidad angular media es igual a la mitad de la velocidad angular final. De lo que sigue que la energía cinética rotacional dada al volante es igual al trabajo realizado por el par.