Modelo de Sólido de Einstein

Un paso útil encaminado al entendimiento del calor específico de los sólidos, fué propuesto por Einstein en 1907, que consideraba al sólido como si estuviera formado por un gran número de osciladores idénticos. El enfoque cuántico del oscilador armónico, da una serie de osciladores con estados cuantizados separados por la misma distancia hf, donde h es la constante de Planck y f es la frecuencia del oscilador. El dibujo de abajo, visualiza un grupo de osciladores uniformemente espaciados en un sólido, despreciando para este estudio cualquier interacción entre ellos.

El sólido de Einstein conceptual, es útil para examinar la idea de la multiplicidad, en la distribución de energía entre los estados de energía disponibles del sistema. Todos los niveles de energía se consideran igualmente probables, con la obligación de tener q unidades de energía y N osciladores.

Como ejemplo, consideremos q = 3 unidades de energía, distribuida en un sólido de Einstein con N = 4 osciladores.

A la izquierda, tenemos una lista detallada de las posibles distribuciones de energía. Un total de 20 distribuciones diferentes para 3 unidades de energía entre 4 osciladores (una multiplicidad de 20). Si tratamos de desarrollar una descripción de un sólido real, con un número de Avogadro de osciladores, esta clase de enfoque es claramente inviable. Afortunadamente las expresiones matemáticas de la multiplicidad, hacen manejable esta tarea. La multiplicidad para q unidades de energía entre N osciladores está dada por la expresión: 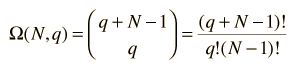La cual para este ejemplo viene a ser Mayor Detalle sobre la Expresión de la Multiplicidad.

La entropía del sólido de Einstein se puede expresar en términos de la multiplicidad.

Para hacer manejable la expresión de la entropía, consideramos los siguientes pasos:

The numbers q and N are presumed large and the 1 is dropped. Ahora, haciendo uso de la aproximación de Stirling para evaluar los factoriales

Haciendo la suposición física de que el número de unidades de energía es mucho mas grande que el número de osciladores, q>>N, la expresión se puede simplificar mas. Reagrupando

Los pasos de arriba hacen uso de las reglas de combinación de logaritmos y la expansión de series de ln(1+N/q) que se puede aproximar por el primer término cuando q>>N: (aproximadamente, ln(1+x)=x si x<<1).

Sustituyendo nos da la expresión de la entropía del sólido de Einstein:

Por último, podemos establecer una conexión con algo parecido a un sólido en el mundo real. La energía interna U se puede representar por q multiplicado por la unidad de energía del oscilador hf= ε. El último término de arriba, será despreciable bajo el supuesto de que q>>N, de modo que la expresión de la entropía queda como

Usando la definición de temperatura como función de la entropía, resulta

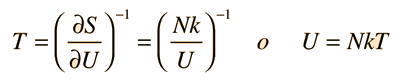
Esto es lo que se esperaba de la equipartición de la energía. Cada oscilador tiene dos grados de libertad, y cada uno representaría kT/2 de energía, dando U=NkT.