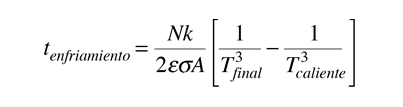Enfriamiento Radiativo de un Fragmento Volcánico

Para el caso ideal de un objeto que se mantiene a una temperatura uniforme, el tiempo de enfriamiento radiativo, sin limitación de transferencia de calor desde el interior del objeto, está dado por:

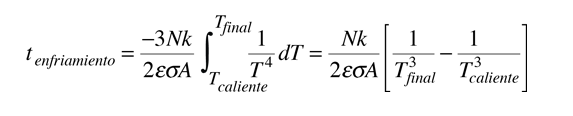
Hay que tener en cuenta que para objetos macroscópicos, el tiempo de enfriamiento calculado para el objeto como un todo, siempre será más corto que el tiempo de enfriamiento real, por lo que aquel será una cota inferior. La relación anterior supone una conductividad térmica infinita, para que la temperatura de todo el objeto sea igual a la temperatura de la superficie. En el mundo real, la superficie se enfría más rápido que el interior. La tasa de transferencia de calor desde el interior, se espera que limite la tasa de pérdida por radiación de la superficie.

A pesar de todas estas limitaciones del mundo real, es interesante tratar de modelar el proceso de enfriamiento de un objeto caliente. La dra. Pam Burnley del Departamento de Geología GSU, tiene un fragmento de material basáltico, que se encontró a unos 60 metros de la cima de un pequeño cono volcánico. El material tiene la apariencia de haber sido expulsado en un estado casi líquido, pero en el impacto, un extremo del fragmento chocó contra el suelo y se dobló. Esto parece implicar que durante su vuelo fuera del cono, se enfrió lo suficiente para solidificarse parcialmente antes del impacto.

Estas dos vistas del fragmento muestran sus dos caras, y la impresión general es que se trataba de algo bastante blando que se dobló por el impacto. Parece una especie de goterón de material volcánico. La dra. Burnley se refiere a él como una "bomba" de volcán.

Datos básicos recogidos de la muestra: Su masa es de 367,6 gramos. Mide unos 17 cm. de largo por 5,5 cm. de ancho y unos 3,5 cm. de grueso. Sumergido en agua, su masa efectiva (peso sumergido) fué de 161 gramos, de modo que por el principio de Arquímedes, su volumen es de 206,6 cm³. Esto le supone una densidad de 1,78 gm/cm³, comparado con una densidad de alrededor de 3 gm/cm³ del basalto sólido, de modo que alberga un montón de aire. La dra. Burnley estimó una temperatura en su estado líquido de unos 1.200 ºC., y unos 1.000ºC., en su estado sólido. De modo que parecen ser valores plausibles, que tomamos como temperaturas caliente y fría en este proceso de modelación.

Modelación de Enfriamiento Radiativo de una Esfera Caliente

El modelado del tiempo de enfriamiento por radiación de una esfera caliente, nos puede dar algunas ideas sobre el papel de la radiación en el enfriamiento de los objetos calientes. La radiación no es definitivamente el único mecanismo implicado, el enfriamiento de los objetos macroscópicos reales es un tema multifacético, incluyendo la transferencia de calor desde el interior del objeto a la superficie. Con esta advertencia acerca de la aplicabilidad de estos resultados en el mundo real, se desarrollará un modelo del enfriamiento radiativo de una esfera. El modelo del tiempo de enfriamiento está dado por

Para una esfera de radio r = cm = m = x 10^m,

El área de la superficie es A = cm² = x 10^ m².

el volumen es V = cm³ = x 10^ m³.

Si la densidad es gm/cm³ = kg/m³, entonces

la masa será gm = kg = x10^ kg.

Si se conoce la masa molar M = gm, entonces se puede determinar el número de átomos o moléculas contenidas en la esfera. (¡Atención! Se asumen que estos son números experimentales. La masa molar y la densidad no son independientes, y es fácil elegir valores que sean incompatibles. Ni tampoco por la masa molar se puede determinar de forma precisa la densidad, debido a diferentes estructuras de cristal, etc.). Con estas suposiciones, el número de partículas es

= x10^

Si la temperatura alta original es = K

entonces un tiempo de enfriamiento de seg. = x10^ seg.

de un objeto con emisividad

corresponde a una temperatura final K

En este cálculo se pueden cambiar los valores de cualquier parámetro, y el cálculo por defecto será sobre la temperatura final. Sin embargo, si se cambia la temperatura final, se calculará el correspondiente tiempo de enfriamiento.

Aunque sea instructivo como exploración, este cálculo no es realista debido a varios supuestos de simplificación:

• Se presume que la masa total está a la misma temperatura, mientras que en cualquier objeto la superficie se enfria mas rapidamente, y por tanto habrá un retraso en la transferencia de calor desde el interior hacia la superficie de radiación.
• Se desprecia el efecto de la temperatura ambiente. Esto puede estar justificado. Si la temperatura del objeto es mas de unas tres veces la del ambiente, entonces el error por este supuesto está por debajo del 1%.
• Se desprecian otros procesos de transferencia de calor como los de conducción y convección. Para temperaturas por encima de 1.000ºK., esto esta probablemente justificado. La conducción y la convección dependen linealmente de la temperatura, mientras que la radiación está relacionada con la cuarta potencia de ella.
• La derivada de la energía respecto de la tempertaura de arriba, está considerablemente simplificada. Esta derivada es realmente el calor específico del objeto, que es mas complejo que esta simple expresión.