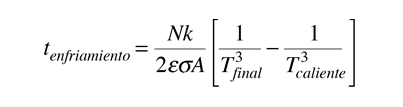Tiempo de Enfriamiento por Radiación

La tasa de emisión de energía de radiación por una superficie caliente, está determinada por la ley de Stefan-Boltzmann .

Aquí P es la potencia emitida por el área, y E es la energía contenida en el objeto. Para objetos muy calientes, se puede despreciar el papel de la temperatura ambiente. Si la temperatura caliente es más de 3,16 veces la temperatura ambiente, entonces la contribución por los términos del ambiente es inferior al 1%. Por ejemplo, para un ambiente en la tierra de 300ºK., un objeto de temperatura superior a 1000ºK., puede ser tratado como un radiador puro en el espacio. Si la pérdida de calor es puramente radiada, y no está limitada por la transferencia de calor desde el interior a la superficie radiante, entonces se puede modelar el tiempo de enfriamiento de un objeto caliente.

Si la energía del objeto se puede representar por energía cinética de traslación pura de acuerdo con la equipartición de energía, entonces

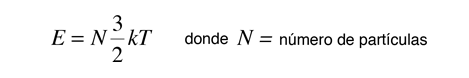
Usando la regla de la cadena de las derivadas

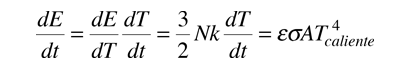
Reagrupando y despejando nos da

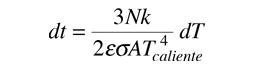
y por integración obtenemos el tiempo de enfriamiento

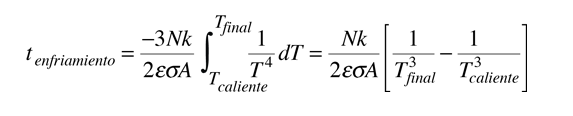
Hay que tener en cuenta que para objetos macroscópicos, el tiempo de enfriamiento calculado para el objeto como un todo, siempre será más corto que el tiempo de enfriamiento real, por lo que aquel le da una cota inferior. La fórmula de arriba asume una conductividad térmica infinita, de modo que la temperatura del objeto en cada lugar es igual a la temperatura superficial. En el mundo real, la superficie se enfriará más rápido que el interior. La tasa de transferencia de calor desde el interior, se espera que limite la tasa de pérdida por radiación de la superficie.

Modelo de Enfriamiento de una Esfera Caliente por Radiación

La modelación del tiempo de enfriamiento por radiación de una esfera caliente, nos puede proporcionar algunas ideas sobre el papel de la radiación en el enfriamiento de los objetos calientes. La radiación no es definitivamente el único mecanismo implicado, el enfriamiento de los objetos macroscópicos reales es un tema multifacético, incluyendo la transferencia de calor desde el interior del objeto hacia la superficie. Con esta advertencia acerca de la aplicabilidad de estos resultados en el mundo real, se desarrollará un modelo para el enfriamiento de una esfera mediante la radiación. El modelo del tiempo de enfriamiento está dada por

Para una esfera de radio r = cm = m = x 10^m,

y un área de superficie A = cm² = x 10^ m².

el volumen es V = cm³ = x 10^ m³.

Si la densidad es gm/cm³ = kg/m³, entonces

la masa será gm = kg = x10^ kg.

Si se conoce la masa molar M = gms., entonces podemos determinar el número de átomos o moléculas contenidos en la esfera. (¡Aviso!. Se suponen que son números experimentales. La masa molar y la densidad no son independientes, y resulta facil elegir valores que son incompatibles. Tampoco la densidad se determina de forma precisa por la masa molar, debido a las diferentes estructuras de cristal, etc. ). Con estas suposiciones, el número de partículas se espera que sea

= x10^

Si la temperatura caliente original es = K.

entonces el tiempo de enfriamiento de seg. = x10^ seg.

para un objeto con emisividad

corresponde a una temperatura final K.

En este cálculo se puede cambiar el valor de cualquier parámetro y la temperatura final se calculará por defecto. Sin embargo, si se cambia la temperatura final, se calculará el correspondiente tiempo de enfriamiento.

Aunque sea instructivo como exploración, este cálculo no es realista debido a varios supuestos de simplificación:

• Se presume que la masa total está a la misma temperatura, mientras que en cualquier objeto la superficie se enfria mas rapidamente, y por tanto habrá un retraso en la transferencia de calor desde el interior hacia la superficie de radiación.
• Se desprecia el efecto de la temperatura ambiente. Esto puede estar justificado. Si la temperatura del objeto es mas de unas tres veces la del ambiente, entonces el error por este supuesto está por debajo del 1%.
• Se desprecian otros procesos de transferencia de calor como los de conducción y convección. Para temperaturas por encima de 1.000ºK., esto esta probablemente justificado. La conducción y la convección dependen linealmente de la temperatura, mientras que la radiación está relacionada con la cuarta potencia de ella.
• La derivada de la energía respecto de la tempertaura de arriba, está considerablemente simplificada. Esta derivada es realmente el calor específico del objeto, que es mas complejo que esta simple expresión.