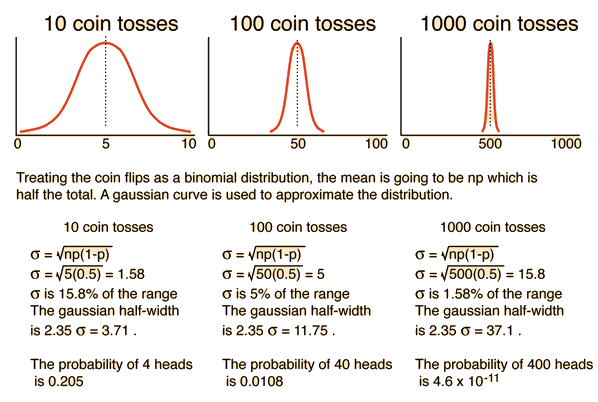
Physical Applications of Distribution Functions
Fundamental to our understanding of classical molecular phenomena is the Boltzmann distribution, which tells us that the probability that any one molecule will be found with energy E decreases exponentially with energy; i.e., any one molecule is highly unlikely to grab much more than its average share of the total energy available to all the molecules. Mathematically, the Boltzmann distribution can be written in the form
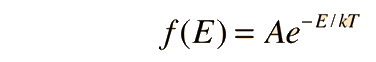 |
|
This distribution can be made plausible by a numerical example, particularly when put in graphical form, but the rigorous mathematical development by Boltzmann still stands as a major achievement in the mathematics of physics. We will take it as a postulate in the development of physical models in kinetic theory.
This idea that each "particle" is unlikely to have much more or less than its "fair share" of the energy can be extended to "modes" in wave phenomena such as the electromagnetic wave modes in a cavity, although this application shows its classical limitations in the Rayleigh-Jeans law.
Another idea contained in the Boltzmann distribution above is that if the general "energy economy" is improved by increasing the temperature so that the total energy available to the particles is increased, a given particle is more likely to get a specified amount of energy. If the overall financial economy of the country is better with more money in circulation, then for any particular financial threshold you picked, there would be a higher probability that any given individual would reach that threshold. By analogy, if there is some particular threshold energy for a given phenomenon, such as ionization or excitation of vibrational states, then the likelihood of that phenomenon happening will increase with temperature in a generally predictable way.
The statistical behavior of many-particle systems is described by the product of the density of states and the distribution function for these states. (See energy distribution as an example.) One of the simplest cases is that for radioactive decay since you are dealing with pure probability. The density of states can just be taken as a constant since there is no preference for one decay time over another, and the distribution function is simply

For the speed of molecules in a gas, however, the density of states can be modeled as an effective "volume" in "velocity space" which gives it the form

so that the distribution arising from the Boltzmann foundation is
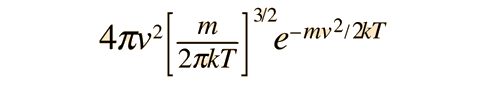
| Comment on statistical methods in physics |
Kinetic theory concepts