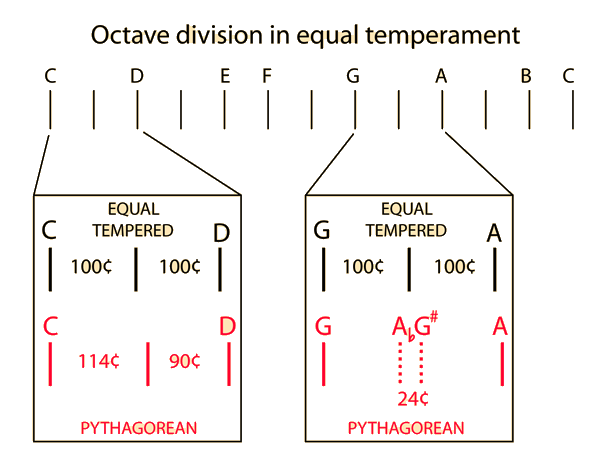
The Equal Tempered Octave


The middle octave on the piano is shown as a standard example of equal temperament. Since a musical interval is defined by a ratio, the division of an octave into 12 equal intervals (equal tempered semitones) involves finding the ratio by which you multiply the starting frequency f twelve times to get a frequency 2f. If this ratio is represented by a, then
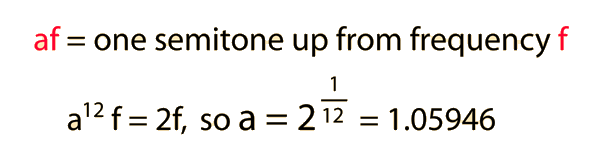
Proceeding up the equal tempered scale, each note is about 6% higher than the previous note.
| Equal tempered octave vs other temperaments |
| Equal tempered frequency list |
Temperament and musical scales
| HyperPhysics***** Sound | R Nave |