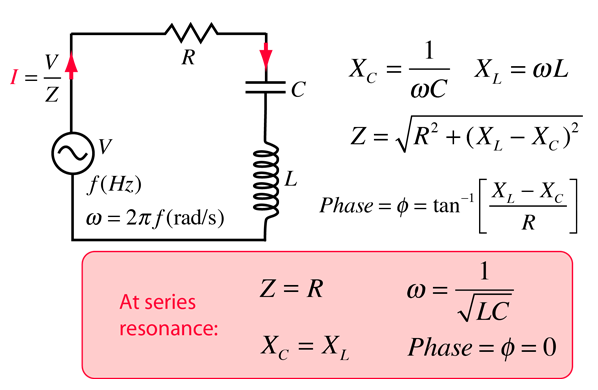
RLC Series Circuit
The RLC series circuit is a very important example of a resonant circuit. It has a minimum of impedance Z=R at the resonant frequency, and the phase angle is equal to zero at resonance.
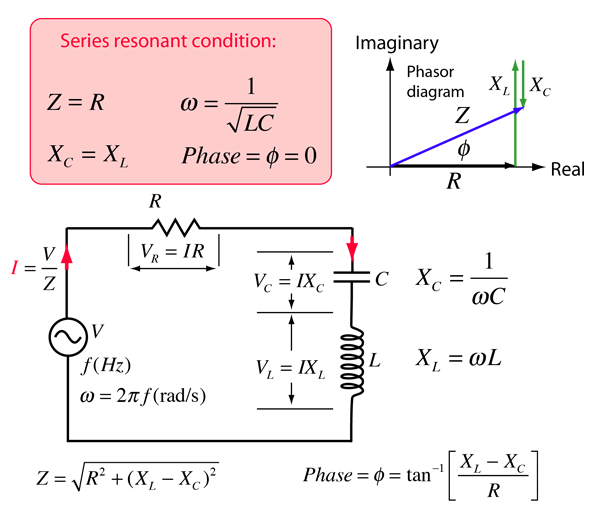
One way to visualize the behavior of the RLC series circuit is with the phasor diagram shown in the illustration above. The phasor diagram shown is at a frequency where the inductive reactance is greater than that of the capacitive reactance. This would occur at a frequency above the resonant frequency.
| Calculation |
Capacitance concepts
Inductance concepts
AC circuit concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |