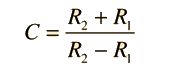Spherical Aberration
For lenses made with spherical surfaces, rays which are parallel to the optic axis but at different distances from the optic axis fail to converge to the same point. For a single lens, spherical aberration can be minimized by bending the lens into its best form. For multiple lenses, spherical aberrations can be canceled by overcorrecting some elements. The use of symmetric doublets like the orthoscopic doublet greatly reduces spherical aberration.
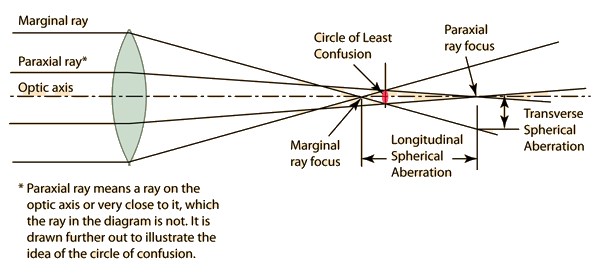
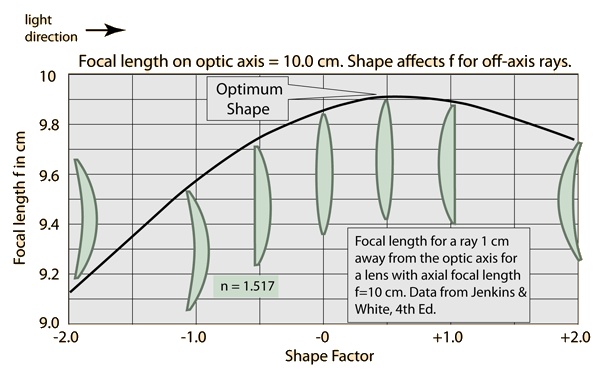
When the concept of principal focal length is used, the presumption is that all parallel rays focus at the same distance, which is of course true only if there are no aberrations. The use of the lens equation likewise presumes an ideal lens, and that equation is practically true only for the rays close to the optic axis, the so-called paraxial rays. For a lens with spherical aberration, the best approximation to use for the focal length is the distance at which the difference between the paraxial and marginal rays is the smallest. It is not perfect, but the departure from perfect focus forms what is called the "circle of least confusion". Spherical aberration is one of the reasons why a smaller aperture (larger f-number) on a camera lens will give a sharper image and greater depth of field since the difference between the paraxial and marginal rays is less.
| Lens Aberrations |
Lens concepts
Thick lens concepts
| HyperPhysics***** Light and Vision | R Nave |