Lens in Different Media

Tracing the vergence is a convenient way to locate the image formed by a thick lens in media of different indices of refraction. The Cartesian sign convention is used.

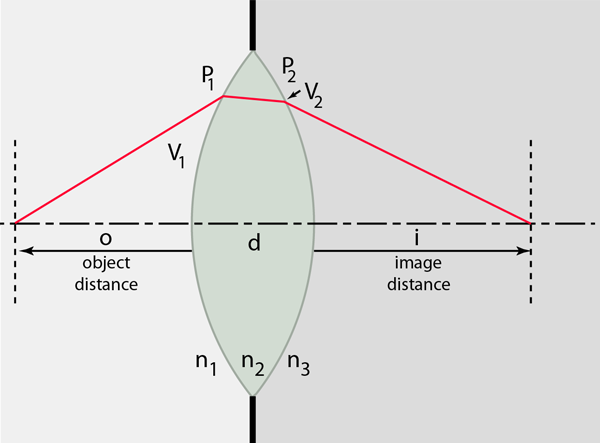
Thick lenses can be analyzed in terms of vergence. The vergence can be traced by noting its change at each surface.

For this case of a thick lens in different media, the system can be characterized by its radii of curvature, its indices of refraction, and its thickness.

A set of default parameters has been set up so that when you enter a value for one of the parameters, those default values will be assigned to the other parameters and the calculation will proceed with those values. Any of the physical parameters can be changed and the change of any entry will initiate the program operation again.

Recommendation: Enter the value n_lens = 1.5 and lens thickness d=1 cm to be consistent with the default set of physical parameters. The calculation will fill in the default physical parameters and calculate the resultant values. Any of the physical parameters can then be changed and the change of any entry will initiate the program operation again.

This glass lens with index
n_lens = n₂ = is embedded in a
front medium of index n₁ =
and a back medium with index n₃ =

the front surface power for lens radius
R₁ = m is given by P₁= (n₂ - n₁)/R₁
P₁ = m^-1

and the back surface power for lens radius
R₂ = m is given by P₂ = (n₃ - n₂)/R₂
P₂ = m^-1

Lens thickness d = cm = m

(Note that for a double convex lens, the front surface radius R₁ is positive and the back surface radius R₂ is negative according to the Cartesian sign convention.)

The vergences can be calculated from the lens parameters and the object distance.The change in vergence when the light encounters a refracting surface is equal to the power of the surface:

Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel.

Object distance o = m.

The vergences can then be calculated.

V₁ = n₁/o = m^-1

V₂ = V₁ + P₁ = n₂/i₁ =m^-1

V₃ = n₂/(i₁ - d) = m^-1

V₄ = V₃ + P₂ = n₃/i =m^-1

The value i₁ calculated as an intermediate value above would be the image distance inside the glass with just the front surface power acting. This calculation presumes that this image distance is greater than the thickness of the lens. It is also presumed that the medium is air so that n₀ = 1.

The exit vergence from the final surface determines the image distance with respect to that surface.

Image distance i = n₃/V₄ = m.

This can be compared with the image distance for a thin lens with the same surface powers:

Image distance i_thin = m.

The power of a thin lens is just the sum of the surface powers:

P_thin = P₁ + P₂ = m^-1.

The equivalent power for the thick lens can be calculated from Gullstrand's equation:

P_thick = P₁ + P₂ - P₁P₂d/n₂ = m^-1.

Note that the calculation does not take into account the change in lens thickness with the angle of the incoming ray. It is typical to do the calculation only for the paraxial rays where the departure from full thickness is negligible. That is why the full thickness d is used in the calculations above. The exaggerated vertical scale of the lens drawing is hopefully helpful visually, but the calculations are not valid except for very small angles for the light paths.

Vergence Example

Index

Lens concepts

Thick lens concepts

Meyer-Arendt
Ch 1.1

HyperPhysics***** Light and Vision

R Nave

Go Back