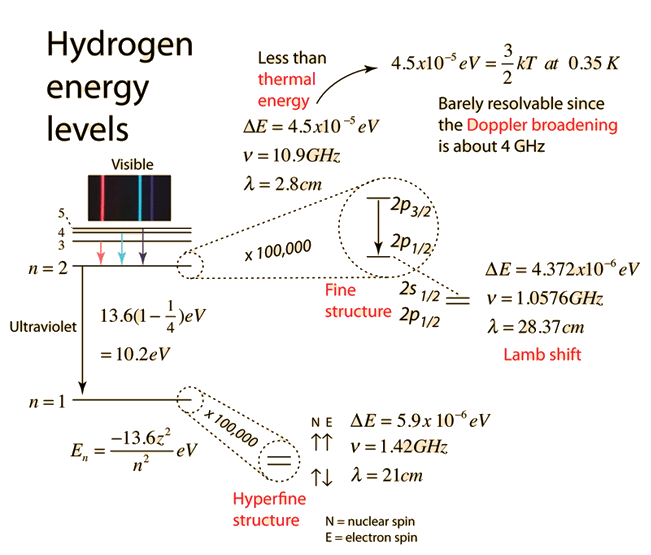Electron Transitions
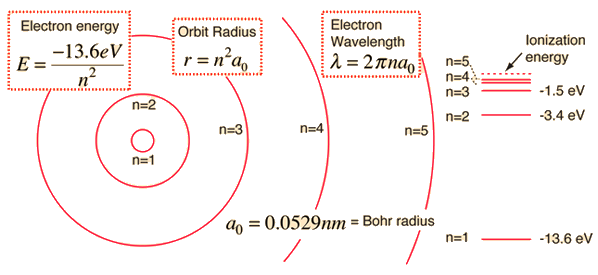
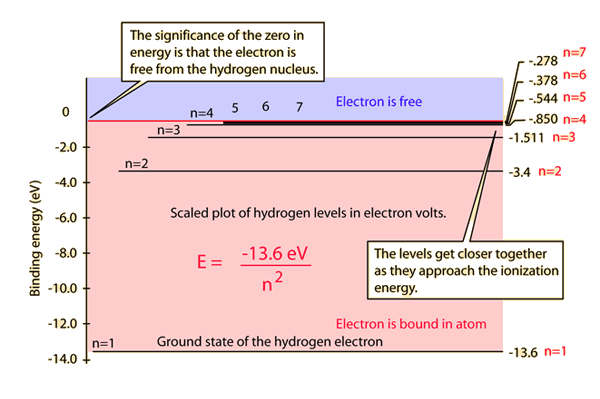
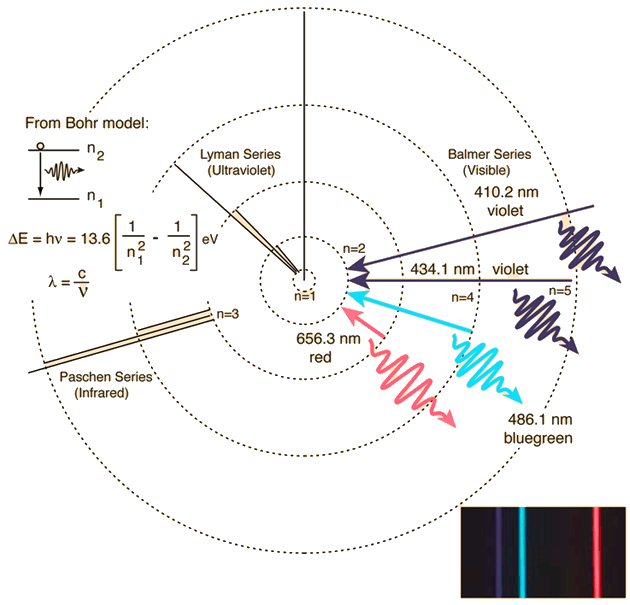
The Bohr model for an electron transition in hydrogen between quantized energy levels with different quantum numbers n yields a photon by emission with quantum energy: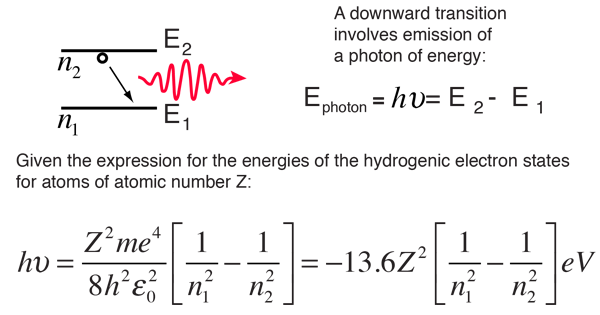
This is often expressed in terms of the inverse wavelength or "wave number" as follows:
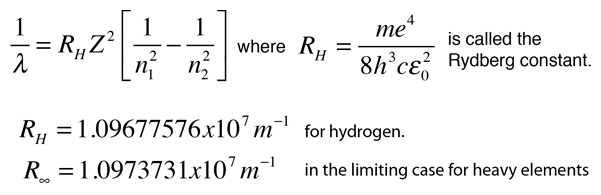
The reason for the variation of R is that for hydrogen the mass of the orbiting electron is not negligible compared to the proton at the high accuracy at which spectral measurement is done. So the reduced mass of the electron is needed. But for heavier elements the movement of the nucleus can be neglected.
Atomic structure concepts
| HyperPhysics***** Quantum Physics | R Nave |