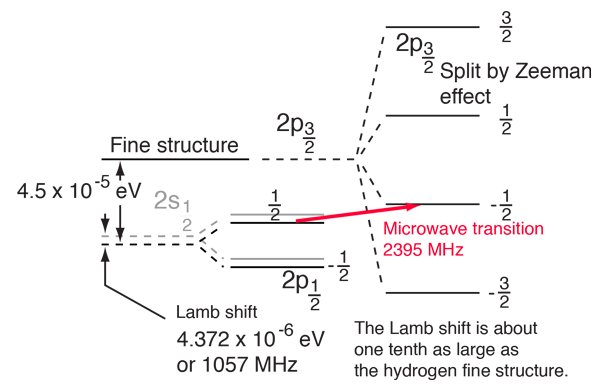
The Lamb Shift
According to the hydrogen Schrodinger equation solution, the energy levels of the hydrogen electron should depend only on the principal quantum number n. In 1951, Willis Lamb discovered that this was not so - that the 2p(1/2) state is slightly lower than the 2s(1/2) state resulting in a slight shift of the corresponding spectral line (the Lamb shift).
It might seem that such a tiny effect would be deemed insignificant, but in this case that shift probed the depths of our understanding of electromagnetic theory. | 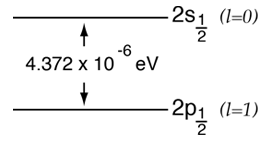 |
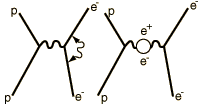 | At the heart of the process is the exchange force by which charges interact by the exchange of photons (the exchange force model of the electromagnetic force). There can be a self-interaction of the electron by exchange of a photon as sketched in the Feynman diagram at left. This "smears out" the electron position over a range of about 0.1 fermi (Bohr radius = 52,900 fermis). This causes the electron spin g-factor to be slightly different from 2. There is also a slight weakening of the force on the electron when it is very close to the nucleus, causing the 2s electron (which has penetration all the way to the nucleus) to be slightly higher in energy than the 2p(1/2) electron. |
When we say the that the penetration of the 2s electron closer to the nucleus leads to an energy higher than that of the 2p, this sounds directly contradictory to the situation with multi-electron atoms. There the penetration of the 2s closer to the nucleus means that it has penetrated inside the 1s electrons and therefore feels a stronger attraction to the positive nucleus, leading to a lower energy level (it takes more energy to remove the 2s from the atom than the 2p). But in the case of the hydrogen atom, there is only one electron, so there is none of the shielding from inner electrons when it is in the 2s or 2p excited states. The effect on the energy levels has an entirely different origin, modeled by quantum electrodynamics. In the absence of this effect, the 2s and 2p would have identical energies since there is no shielding by the presence of other electrons. The "self-interaction" of the electron when it is near the proton causes the effective "smearing" of the electron charge so that its attraction to the proton is slightly weaker than it otherwise would have been. This means it has encountered an interaction which makes it slightly less tightly bound than a 2p electron, hence higher in energy.
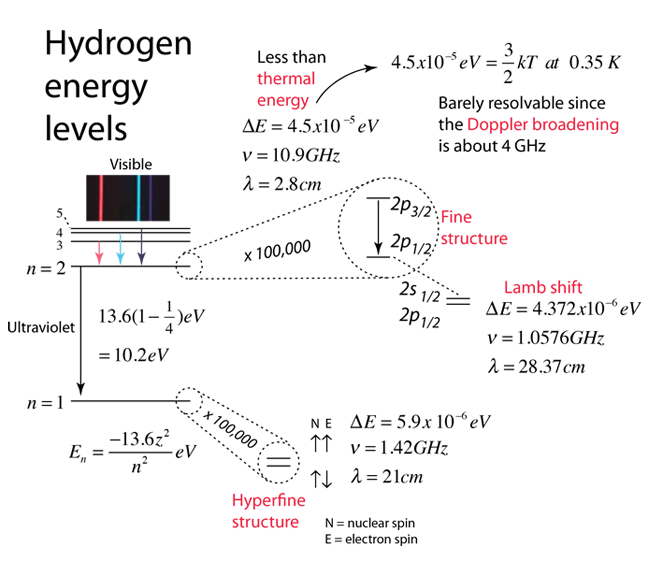
Active illustration: click for more detail
| Microwave measurement of the Lamb shift. | Significance of the Lamb shift |
| Saturation spectroscopy measurement of the Lamb shift. |
Schrodinger equation concepts
Hydrogen concepts
Reference
Rohlf
Sec 8-9.
Lamb Shift Washington.edu
Lamb Shift wiki
| HyperPhysics***** Quantum Physics | R Nave |