Current and Power From a Generated Voltage
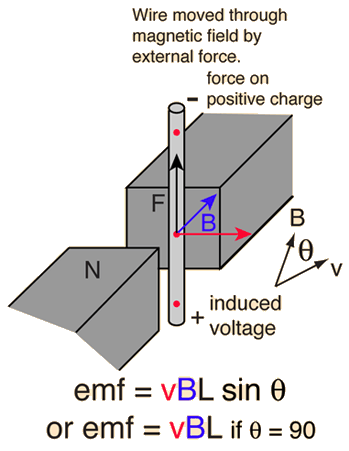 |
When a conductor moves through a magnetic field, there will be a generated motional emf. This is one example of Faraday's Law and it arises from the magnetic force. The voltage generated in a length of wire, presuming that the entire length moves through a uniform field, is given below.
|
If the velocity is perpendicular to the magnetic field then the generated voltage is given by the simple product:
Generated voltage = emf = Velocity x B-field x Length
Electromagnetic force
Magnetic field concepts
| HyperPhysics***** Electricity and Magnetism | R Nave |