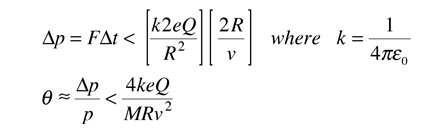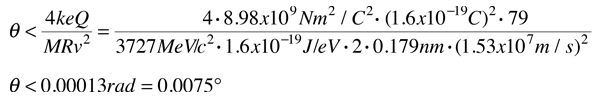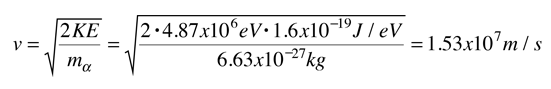Evidence for Nuclear Interaction
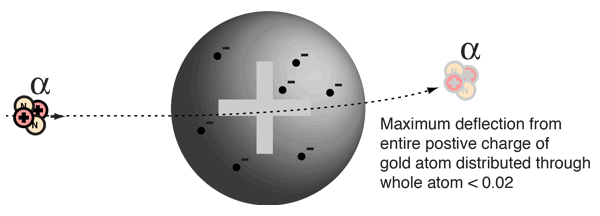
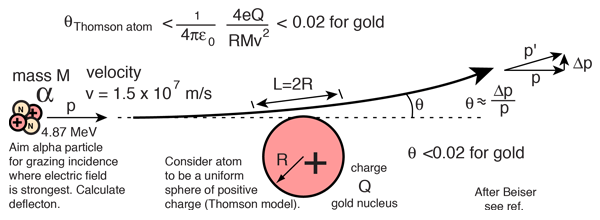
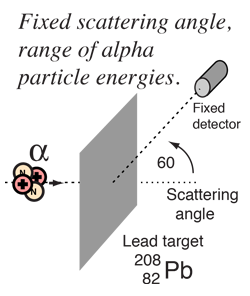
Rutherford and colleagues were able to calculate the number of alpha particles which would be scattered into any angle based upon the number of nuclei and their spacing in the gold foil. The observations agreed with these calculations up to a certain large angle where they got significant deviations. This indicated a new interaction force and was interpreted as "hitting" the nucleus. This scattering angle could be used to calculate the distance of closest approach and therefore the "radius" of the nucleus.
 | The distance from the path of the alpha particle to the centerline is called the impact parameter. The smaller the impact parameter, the larger the angle of deflection. |
Rutherford concepts
| HyperPhysics***** Nuclear | R Nave |