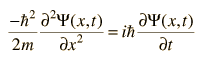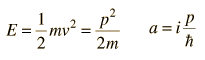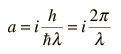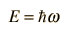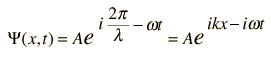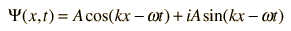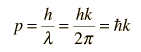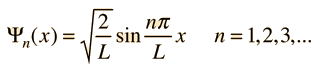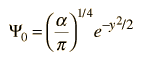Physical Boundary Conditions and the Uniqueness Theorem
For physical applications of quantum mechanics that involve the solution of the Schrodinger equation, such as those of the time independent Schrodinger equation, one must find specific mathematical solutions that fit the physical boundary conditions of the problem.
One very important idea in differential equations is the "uniqueness theorem", which basically says that if you can find a solution to the differential equation that fits the physical boundary conditions of the problem you are considering, then that is in fact the correct solution. That leads to typical comments from students of differential equations like "if you can guess the solution and force it to fit the boundary conditions, then you have the right answer."
The time-independent Schrodinger equation is used for a number of practical problems.
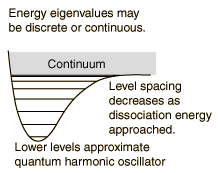
Systems with bound states are related to the quantum mechanical "particle in a box", barrier penetration is important in radioactive decay, and the quantum mechanical oscillator is applicable to molecular vibrational modes.
If, for example, you go to the "particle in a box", you find that for an infinite-walled box the wavefunction must equal zero at the edges of the box, and you can propose a sine wave solution and force it to fit the boundary conditions. How would you know to propose a sine wave solution? Well, in many areas of mathematics and science we "stand on the shoulders of giants" and can make use of the fact that many in the past have explored these kinds of problems and can suggest to us the types of solutions to try. This is part of the nature of applying differential equations to physical problems.
|