Free particle approach to the Schrodinger equation
Though the Schrodinger equation cannot be derived, it can be shown to be consistent with experiment. The most valid test of a model is whether it faithfully describes the real world. The wave nature of the electron has been clearly shown in experiments like the Davisson-Germer experiment. This raises the question "What is the nature of the wave?". We reply, in retrospect, that the wave is the wavefunction for the electron. Starting with the expression for a traveling wave in one dimension, the connection can be made to the Schrodinger equation. This process makes use of the deBroglie relationship between wavelength and momentum and the Planck relationship between frequency and energy.
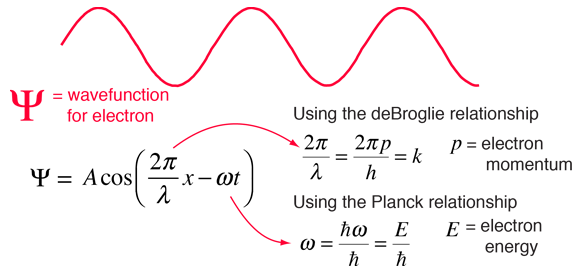
It is easier to show the relationship to the Schrodinger equation by generalizing this wavefunction to a complex exponential form using the Euler relationship. This is the standard form for the free particle wavefunction.
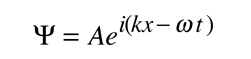
If we now take the partial derivatives of this wavefunction with respect to position and time, we can show that these derivatives are related to momentum and energy respectively.
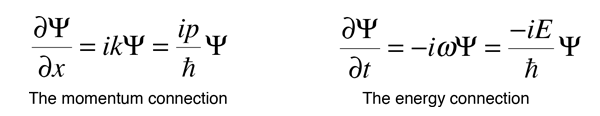
When an operation on a function gives back a constant times the function, that constant is called an eigenvalue, and the function is an eigenfunction. The above relationships can be rearranged as follows.
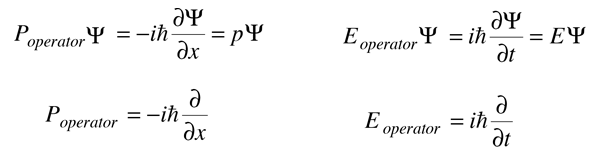
In this kind of fashion, quantum mechanical "operators" can be developed for relevant physical observables.
The connection to the Schrodinger equation can be made by examining wave and particle expressions for energy:

Asserting the equivalence of these two expressions for energy and putting in the quantum mechanical operators for both brings us to the Shrodinger equation
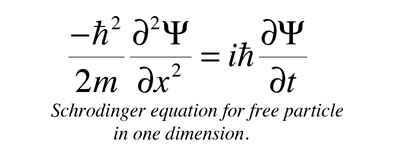
Schrodinger equation concepts
| HyperPhysics***** Quantum Physics | R Nave |