Quantum Harmonic Oscillator: Ground State Solution

To find the ground state solution of the Schrodinger equation for the quantum harmonic oscillator

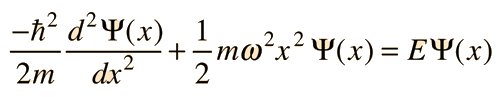
we try the following form for the wavefunction

Substituting this function into the Schrodinger equation by evaluating the second derivative gives

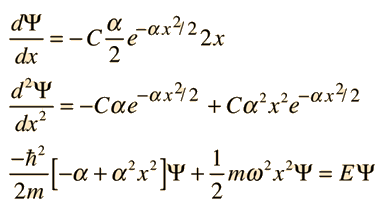
For this to be a solution to the Schrodinger equation for all values of x, the coefficients of each power of x must be equal. That gives us a method for fitting the boundary conditions in the differential equation. Setting the coefficients of the square of x equal to each other:

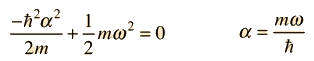
Then setting the constant terms equal gives the energy

This is the smallest energy allowed by the uncertainty principle. Show

This is a very significant physical result because it tells us that the energy of a system described by a harmonic oscillator potential cannot have zero energy. Physical systems such as atoms in a solid lattice or in polyatomic molecules in a gas cannot have zero energy even at absolute zero temperature. The energy of the ground vibrational state is often referred to a "zero point vibration". The zero point energy is sufficient to prevent liquid helium-4 from freezing at atmospheric pressure, no matter how low the temperature.