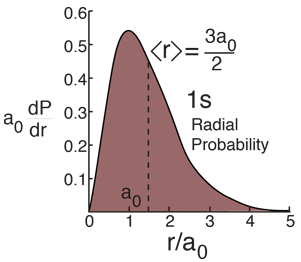
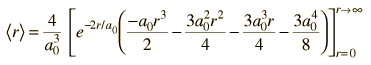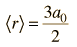The Most Probable Radius
Hydrogen Ground State
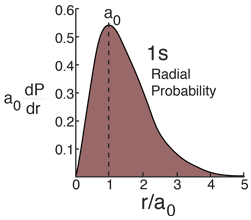 |
The radial probability density for the hydrogen ground state is obtained by multiplying the square of the wavefunction by a spherical shell volume element.  It takes this comparatively simple form because the 1s state is spherically symmetric and no angular terms appear. |
Dropping off the constant terms and taking the derivative with respect to r and setting it equal to zero gives the radius for maximum probability.
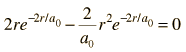
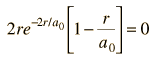
which gives

where
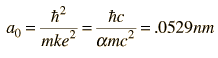
The most probable radius is the ground state radius obtained from the Bohr theory. The Schrodinger equation confirms the first Bohr radius as the most probable radius but goes further to describe in detail the profile of probability for the electron radius.
| Probability for a radial range |
| Expectation value for radius |
Schrodinger equation concepts
Hydrogen concepts
| HyperPhysics***** Quantum Physics | R Nave |