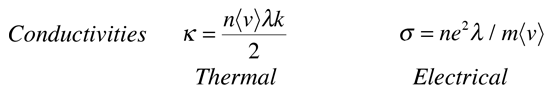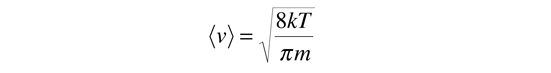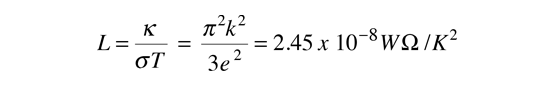Thermal Conductivity
Heat transfer by conduction involves transfer of energy within a material without any motion of the material as a whole. The rate of heat transfer depends upon the temperature gradient and the thermal conductivity of the material. Thermal conductivity is a reasonably straightforward concept when you are discussing heat loss through the walls of your house, and you can find tables which characterize the building materials and allow you to make reasonable calculations.
More fundamental questions arise when you examine the reasons for wide variations in thermal conductivity. Gases transfer heat by direct collisions between molecules, and as would be expected, their thermal conductivity is low compared to most solids since they are dilute media. Non-metallic solids transfer heat by lattice vibrations so that there is no net motion of the media as the energy propagates through. Such heat transfer is often described in terms of "phonons", quanta of lattice vibrations. Metals are much better thermal conductors than non-metals because the same mobile electrons which participate in electrical conduction also take part in the transfer of heat.
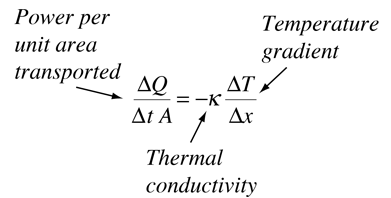
Conceptually, the thermal conductivity can be thought of as the container for the medium-dependent properties which relate the rate of heat loss per unit area to the rate of change of temperature.
 |
|
For an ideal gas the heat transfer rate is proportional to the average molecular velocity, the mean free path, and the molar heat capacity of the gas.
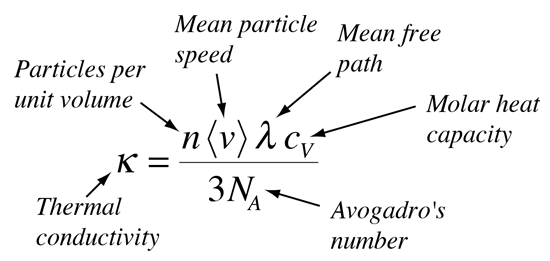
For non-metallic solids, the heat transfer is view as being transferred via lattice vibrations, as atoms vibrating more energetically at one part of a solid transfer that energy to less energetic neighboring atoms. This can be enhanced by cooperative motion in the form of propagating lattice waves, which in the quantum limit are quantized as phonons. Practically, there is so much variability for non-metallic solids that we normally just characterize the substance with a measured thermal conductivity when doing ordinary calculations.
For metals, the thermal conductivity is quite high, and those metals which are the best electrical conductors are also the best thermal conductors. At a given temperature, the thermal and electrical conductivities of metals are proportional, but raising the temperature increases the thermal conductivity while decreasing the electrical conductivity. This behavior is quantified in the Wiedemann-Franz Law:
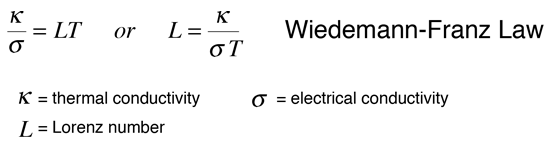
where the constant of proportionality L is called the Lorenz number. Qualitatively, this relationship is based upon the fact that the heat and electrical transport both involve the free electrons in the metal. The thermal conductivity increases with the average particle velocity since that increases the forward transport of energy. However, the electrical conductivity decreases with particle velocity increases because the collisions divert the electrons from forward transport of charge. This means that the ratio of thermal to electrical conductivity depends upon the average velocity squared, which is proportional to the kinetic temperature.
| Thermal conductivity table |
Heat transfer concepts
Heat transfer examples
| HyperPhysics***** Thermodynamics | R Nave |