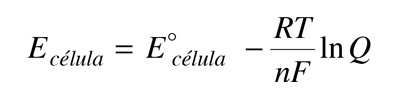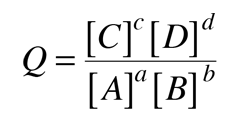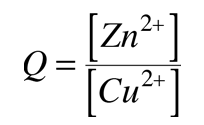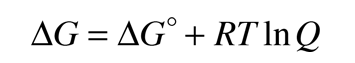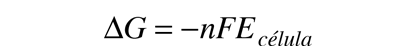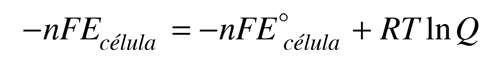Potenciales de Electrodo Estándares
En una célula electroquímica, se crea un potencial eléctrico entre dos metales diferentes. Este potencial es una medida de la energía por unidad de carga que está disponible a partir de las reacciones de oxidación/reducción para impulsar la reacción. Es costumbre visualizar la reacción celular en términos de dos semireacciones, una semireacción de oxidación y una semireacción de reducción.
| Especies reducidas -> especies oxidadas + ne- | |
| Especies oxidadas + ne- -> especies reducidas | |
El potencial de célula (a menudo llamado la fuerza electromotriz o fem) tiene una contribución desde el ánodo, que es una medida de su capacidad para perder electrones - que se denomina su "potencial de oxidación" -. El cátodo tiene una contribución en base a su capacidad para ganar electrones, su "potencial de reducción". El potencial de la célula se puede escribir entonces como
Ecélula = potencial de oxidación + potencial de reducción
Si pudieramos tabular los potenciales de oxidación y reducción de todos los electrodos disponibles, entonces podríamos predecir los potenciales de célula de las células voltaicas creadas a partir de cualquier par de electrodos. En realidad, la tabulación de uno u otro es suficiente, ya que el potencial de oxidación de una semirreacción es el negativo del potencial de reducción de la inversa de esa reacción. Dos obstáculos principales se deben superar para establecer dicha tabulación
- El potencial de electrodo no se puede determinar de forma aislada, sino en reacción con algún otro electrodo.
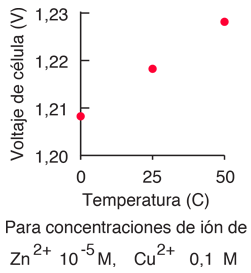
- El potencial del electrodo depende de las concentraciones de las sustancias, la temperatura, y la presión en el caso de un electrodo de gas.
En la práctica, el primero de estos obstáculos se supera mediante la medición de los potenciales con respecto a un electrodo de hidrógeno estándar. La naturaleza del potencial eléctrico determina que el cero de potencial sea arbitrario, pero la diferencia de potencial es la que tiene consecuencia práctica. La tabulación de todos los potenciales de electrodos con respecto al mismo electrodo estándar, proporciona un marco de trabajo práctico para una amplia gama de cálculos y predicciones. Al electrodo de hidrógeno estándar se le asigna un potencial de cero voltios.
El segundo obstáculo es superado por la elección de las condiciones termodinámicas estándares para la medición de los potenciales. Los potenciales de electrodo estándar se determinan habitualmente en concentraciones de soluto de 1 Molar, presiones de gas de 1 atmósfera, y una temperatura estándar, que es por lo general 25°C. El potencial de célula estándar se denota por un signo de grado en el superíndice.
| E°célula | - Medido contra el electrodo de hidrógeno estándar.
- Concentración 1 Molar
- Presión 1 atmósfera
- Temperatura 25ºC
|
El ejemplo siguiente muestra algunos de los valores extremos de potenciales de célula estándar.
Cátodo (reducción)
Semi-reacción | Potencial estandar
E° (voltios) |
| Li+(aq) + e- -> Li(s) | -3,04 |
| K+(aq) + e- -> K(s) | -2,92 |
| Ca2+(aq) + 2e- -> Ca(s) | -2,76 |
| Na+(aq) + e- -> Na(s) | -2,71 |
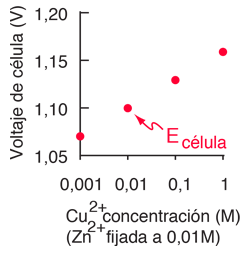
| Zn2+(aq) + 2e- -> Zn(s) | -0,76 |
| Cu2+(aq) + 2e- -> Cu(s) | 0,34 |
| O3(g) + 2H+(aq) + 2e- -> O2(g) + H2O(l) | 2,07 |
| F2(g) + 2e- -> 2F-(aq) | 2,87 |
Los valores de las entradas de la tabla son los potenciales de reducción, de modo que el litio en la parte superior de la lista tiene el número más negativo, lo que indica que es el agente reductor más fuerte. El agente oxidante más fuerte es el flúor con el mayor número positivo de potencial de electrodo estándar. El siguiente enlace le llevará a una tabla más amplia.
Entre las aplicaciones útiles de los potenciales de electrodo estandar, se incluyen las siguientes.
|
Índice
Conceptos de
Oxidación/
Reducción
Conceptos de Electroquímica
Referencias
Hill & Kolb
Cap. 8
Ebbing
Cap. 19 |