Fracción de Población de Estados Excitados
La distribución de Boltzmann que es fundamental para el entendimiento del fenómeno molecular clásico, nos dice que probabilidad de encontrar una molécula con una energía E, disminuye exponencialmente con la energía; es decir es muy poco probable que cualquier molécula tome mucho mas que la energía promedio del total de la energía disponible para todas las moléculas. Matemáticamente la distribución de Boltzman se puede escribir de la siguiente forma
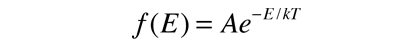 |
|
La fracción de población de un estado excitado, se puede calcular a partir de la distribución de Boltzmann. La distribución de energía depende de la función de distribución y de la densidad de estados disponibles para un nivel de energía determinado. En muchos casos, habrá mas formas de alcanzar un nivel de energía superior, de modo que al calcular las poblaciones, se debe tomar en cuenta el peso estadístico.
El ejemplo de aquí no tendrá en cuenta la densidad de estados, sino que considerará el caso como una colección de partículas puntuales en equilibrio térmico a la temperatura T. Esto nos puede proporcionar algún conocimiento sobre la probabilidad de alcanzar algún umbral del fenómeno físico, o la probabilidad de sobrepasar alguna barrera. Note que esto es un cálculo clásico, y no tiene en cuenta la posibilidad de fenómeno túnel en mecánica cuántica.
Notas del cálculo: Los parámetros sin especificar, tomarán unos valores por defecto, pero se pueden cambiar todos ellos. Si se pone una fracción mayor que 1, también serán sustituidos por valores por defecto. Si por el contrario se especifica una fracción correcta, se calculará la temperatura para una determinada energía.
| Energía Térmica Media |
Conceptos sobre Teoría Cinética
| HyperPhysics*****Termodinámica | M Olmo R Nave |