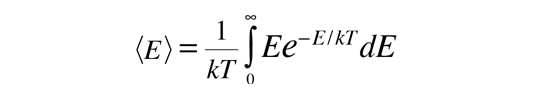Aplicaciones de la Distribución de Boltzmann

Energía de Partícula Media en la Distribución de Boltzmann

La Distribución de Boltzmann describe la distribución de energía entre las partículas clásicas (distinguibles):

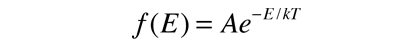
Se puede usar para evaluar la energia media por partícula, en el caso donde no hay densidad de estados dependientes de la energía, que puedan desviar la distribución. Para representar la probabilidad de una energía determinada, se debe normalizar a una probabilidad de 1:

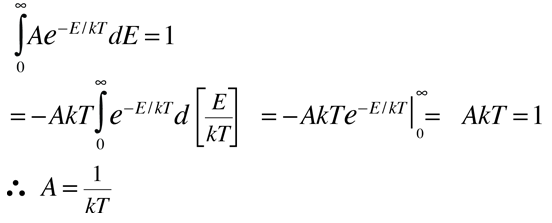
Esta función de distribución normalizada, se puede luego usar para evaluar el valor esperado o energía media.

Mostrar

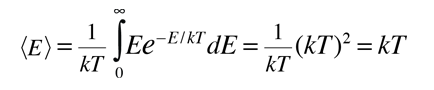Esto muestra que la energía media = kT cuando la energía está aleatoriamente distribuida entre los estados de energía disponibles. El desarrollo de la distribución de Boltzmann, se hizo bajo los supuestos de la conservación de la energía y la conservación del número de partículas. Nótese que esta energía media de la energía distribuida aleatoriamente, no es la misma que la energía cinética media.

Integral de la Energía Media: Distribución de Boltzmann

La integral de la energía media en la distribución de energía sobre una colección de partículas de acuerdo con la distribución de Boltzmann es:

Se puede evaluar esta integral, usando la integración por partes.

Esta técnica es particularmente apropiada para quitar un término lineal, que multiplica a un exponente.