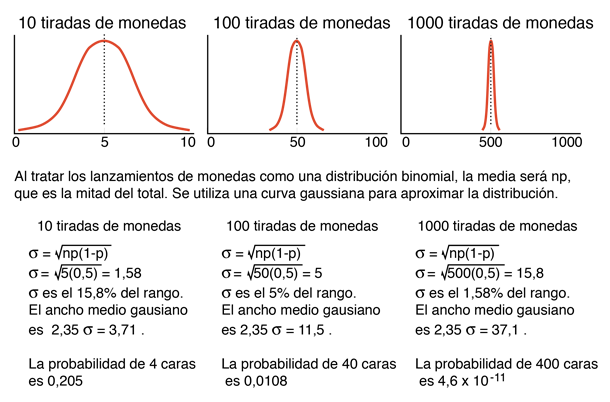
Aplicaciones Físicas de las Funciones de Distribución

La distribución de Boltzmann que es fundamental para el entendimiento del fenómeno molecular clásico, nos dice que la probabilidad de encontrar una molécula con una energía E, disminuye exponencialmente con la energía; es decir es muy poco probable que cualquier molécula tome mucho mas que la energía promedio del total de la energía disponible para todas las moléculas. Matemáticamente la distribución de Boltzman se puede escribir de la siguiente forma

Aplicaciones

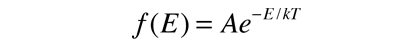Esta distribución se puede estudiar mediante un ejemplo numérico, particularmente cuando se pone en forma gráfica, pero el desarrollo matemático riguroso de Boltzmann se mantiene como un importante logro en las matemáticas de la física. Vamos a tomarlo como un postulado en el desarrollo de modelos físicos en la teoría cinética.

Esta idea de que es poco probable cada "partícula" que tenga más o menos de su "cuota correspondiente" de la energía total, se puede extender a los "modos" en los fenómenos de ondas, como los modos de onda electromagnética en una cavidad, aunque esta aplicación muestra sus limitaciones clásicas en la ley de Rayleigh-Jeans.

Otra de las ideas contenidas en la distribución de Boltzmann anterior es que si aumentando la temperatura se mejora la "economía energética" total, de modo que la energía total disponible para las partículas es mayor, una partícula dada tiene más probabilidades de obtener una cantidad específica de energía. Si la economía financiera global de un país mejora, habrá más dinero en circulación. Entonces, si se hubiera establecido cualquier nivel financiero particular de un individuo, es mas probable que lo obtenga con este aumento de dinero en circulación (mejora económica). Por analogía, dado un determinado umbral de energía para que se produzca un fenómeno como la ionización o la excitación de estados vibracionales, la probabilidad de que eso ocurra, aumentará con el aumento de temperatura, de una manera general predecible.

El comportamiento estadístico de muchos sistemas de partículas, es descrito por el producto de la densidad de estados, por la función de distribución para estos estados. (Ver la distribución de energía como un ejemplo.) Uno de los casos mas simples es el del decaimiento radioactivo, puesto que trata de una probabilidad pura. Se puede tomar la densidad de estados como una constante, puesto que no hay preferencia de un decaimiento sobre otro, y la función de distribución es simplemente

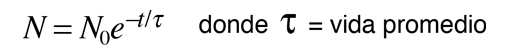
Sin embargo para la velocidad de las moléculas en un gas, se puede modelar la densidad de estados como un "volumen" efectivo en el "espacio de las velocidades", la cual toma la forma

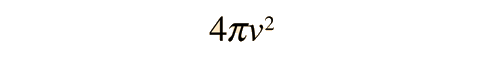
de modo que la distribución que surge del fundamento de Boltzmann es

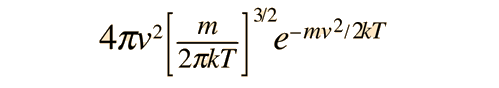
Comentario sobre el Método Estadístico en Física

Si bien puede parecer inquietante describir los fenómenos físicos en el mismo lenguaje que se usa para el lanzamiento de monedas o dados, consideremos que en la descripción de los átomos o moléculas de los sistemas naturales, tenemos un número de acontecimientosen del orden del número de Avogadro. Si estamos conforme con saber las cosas dentro de un cierto margen de error, por ejemplo un 1%, entonces las estadísticas de los grandes números nos la puede dar.

Tomando el lanzamientos de monedas como un ejemplo y utilizando la distribución binomial, sabemos que el número medio de "caras" va a ser el número de lanzamientos (n) multiplicado por la probabilidad (p=0,5), de modo que np = la mitad del total.

En términos de porcentaje de desviación sobre el resultado esperado, está claro que el resultado estadístico de un gran número de eventos es mucho mas preciso.