Aproximación de Stirling para n!
Al evaluar las funciones de distribución en estadísticas, a menudo es necesario evaluar considerables factoriales de números, como en la distribución binomial:
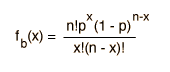
Una relación aproximada útil y de uso común en la evaluación de factoriales de grandes números es la aproximación de Stirling

La siguiente es una aproximación ligeramente mas segura
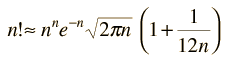
pero en la mayoría de los casos la diferencia es pequeña. Este término adicional, nos proporciona una forma de valorar si la aproximación tiene un error grande.
La aproximación de Stirling es también útil para calcular la aproximación al logaritmo de un factorial, la cual encuentra aplicación en la evaluación de la entropía en términos de la multiplicidad, como en el sólido de Einstein. El logaritmo de n! es

pero normalmente se suele despreciar el último término, de modo que una aproximación que funciona es
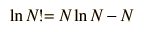
Shroeder da una evaluación numérica de la seguridad de las aproximaciones.
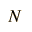 | 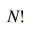 | 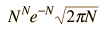 |  | 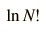 |  |  |
| Relation con la Función Gamma |
Conceptos sobre Estadística
Referencia
Schroeder
App. B
Cap. 2
| HyperPhysics*****HyperMath | M Olmo R Nave |