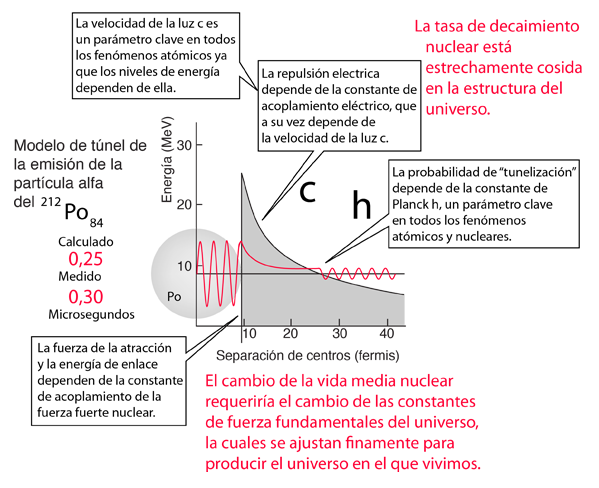
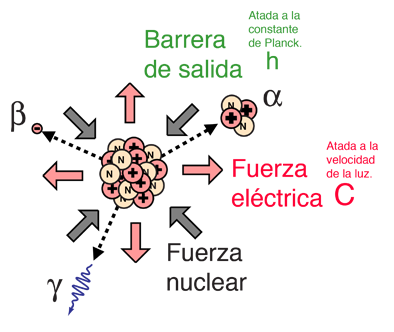
Modelación de la Partícula Alfa del Polonio-212
 |
El increíble rango de semi vidas de decaimiento alfa, se puede modelar con el efecto túnel de la mecánica cuántica. La ilustración de la izquierda representa la barrera enfrentada por una partícula alfa de polonio-212, con una energía de 8,78 MeV y con una semi vida de 0,3 microsegundos. Las siguientes características del entorno nuclear pueden ser calculadas a partir de un modelo básico del núcleo:
|
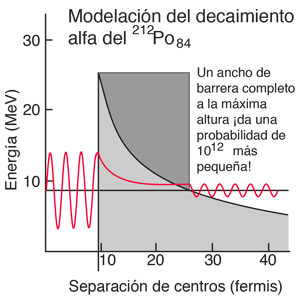
La forma de la barrera obviamente debe tenerse en cuenta, ya que cae rápidamente. Pero es instructivo calcular la semi vida de una barrera rectangular de esa altura y anchura. Usando el cálculo de penetración de barrera da una semi vida de 1,5 x 107 segundos, alrededor de 13 órdenes de magnitud mayor que la vida media observada. Esto da una idea de la amplia gama de vidas medias alfa; la probabilidad de efecto túnel depende muy fuertemente de la naturaleza de la barrera. La probabilidad depende exponencialmente de la altura y la anchura, y en este caso la altura está cayendo con la distancia desde el núcleo en una proporción, 1/r.
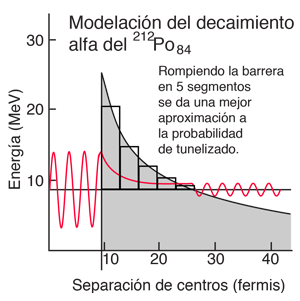 |
Se puede conseguir una mejor probabilidad de efecto túnel, mediante la ruptura de la barrera en segmentos y multiplicando las sucesivas probabilidades de efecto túnel, de acuerdo con las reglas básicas de la combinación de probabilidades. Las probabilidades de efecto túnel calculadas para los segmentos se muestran en la tabla.
|
Cuando se utiliza esta probabilidad de efecto túnel para calcular la semi vida, se obtiene un valor de 0,25 microsegundos. Esto está sorprendentemente cerca del valor medido de 0,3 microsegundos, teniendo en cuenta que una barrera incorrecta, puede dar un resultado que difiera en muchos órdenes de magnitud. Debe admitirse que el mismo cálculo para otros núcleos no produce tal concordancia, pero este ejemplo muestra que las semi vidas observadas, están dentro del rango que se puede calcular a partir del efecto túnel de la mecánica cuántica.
| ¿Que se Puede Hacer para Cambiar la Semi Vida? |
Conceptos de Decaimiento Alfa
Referencias
Rohlf
Sec 7-4
Eisberg & Resnick
Sec 16-2
| HyperPhysics*****Nuclear | M Olmo R Nave |