Fuerzas Fuerte y Electromagnética en el Decaimiento Alfa
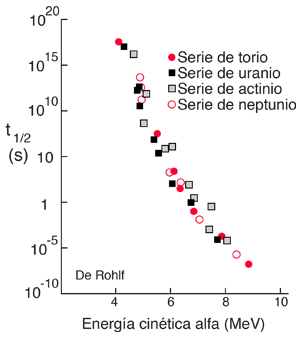
La fuerza nuclear fuerte y la fuerza electromagnética influyen en la radiactividad en forma de desintegración alfa. Al examinar las constantes de acoplamiento de las fuerzas fundamentales, queda claro que se esperaría que la fuerza fuerte dominara los fenómenos dentro del núcleo. Dentro del interior nuclear, la fuerte atracción de fuerza entre los nucleones produce un pozo profundo de energía potencial, aunque para hacerlo debe superar la fuerte repulsión electromagnética de los protones. Sin embargo, la fuerza nuclear fuerte es una fuerza de rango extremadamente corto y esta energía potencial negativa esencialmente desaparece en el radio del núcleo como se ilustra a continuación.
Si una partícula alfa está fuera del núcleo, experimentaría la fuerza repulsiva eléctrica de la carga nuclear positiva, teniendo una gran energía potencial eléctrica como se muestra. La fuerza de Coulomb con su ley del inverso del cuadrado actuaría sobre ella, proporcional a la pendiente de la curva de energía potencial
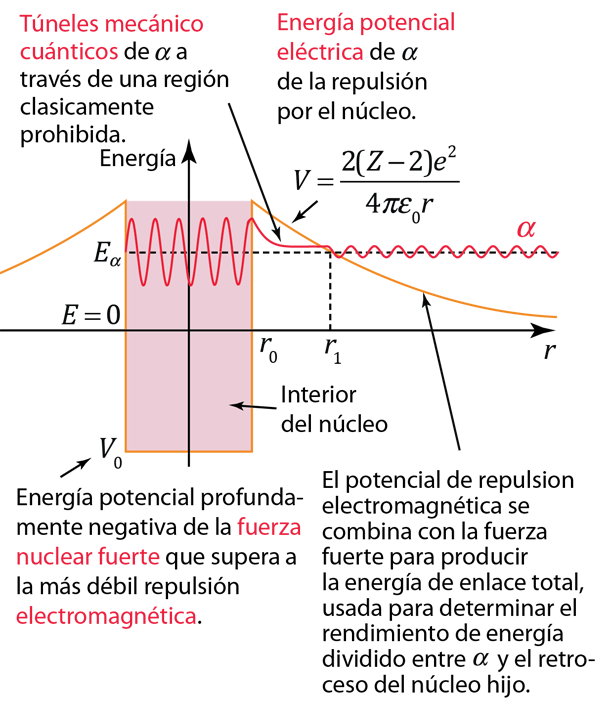
Para explorar más este fenómeno, los pasos serán aproximados y algo cualitativos porque involucran tanto ideas clásicas como cuánticas. Usando el ejemplo de la desintegración alfa del Polonio-212, la altura del potencial eléctrico en el radio nuclear es de aproximadamente 26,4 MeV. La energía medida de la partícula alfa emitida es de 8,78 MeV con una vida media de 0,3 microsegundos.
Para encontrar la energía disponible que darles a las partículas que resultan de la desintegración alfa, se usa la diferencia en la energía de enlace entre el núcleo padre y el hijo. Si la energía de la masa del padre es mayor que la suma de las energías de la masa del núcleo hijo y las partículas emitidas, ese exceso de energía se da a las partículas emitidas más la energía de retroceso del nucleido hijo. Para encontrar este rendimiento energético neto, uno puede simplemente tomar la diferencia entre las masas atómicas de los constituyentes de la desintegración, usando la masa atómica de helio para la partícula alfa. De esta forma, las masas de los electrones se anulan. La conversión de esta diferencia de masa a su equivalente de energía E=mc2 da la energía cinética neta disponible dada a los productos, ya que los efectos tanto de la atracción de fuerza nuclear fuerte como de la repulsión electromagnética se incluyen en esta diferencia de masa atómica. Para la desintegración alfa del polonio-212, las diferencias entre las masas atómicas son:
Q = [m(212Po) -m(4He) - m(208Pb)]u[931,502 MeV/u]
Q = [211,988852u -4,002603u - 207,976627u][931,502 MeV/u] = 8,96 MeV
Teniendo en cuenta el retroceso del núcleo hijo se obtiene la energía cinética de la partícula alfa:
KEα = Q/(1 + mα/m(208Pb)) = 8,79 MeV
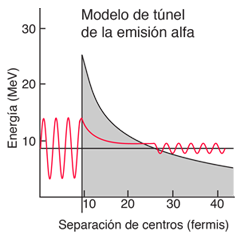
Clásicamente, los 8,78 MeV medidos para la partícula alfa no son suficientes para pasar la barrera de 26,4 MeV. El hecho de que se observe que sale del núcleo es un ejemplo del efecto túnel de la mecánica cuántica que da una pequeña probabilidad de que pueda atravesar la barrera. Para aplicar un modelo de túnel alfa a esta situación, se debe tener en cuenta el hecho de que la función de onda que representa la partícula alfa está decayendo dentro de la barrera. Para un cálculo de modelo aproximado, la barrera se divide en cinco partes y cada una se trata como una barrera rectangular. La vida media depende de la probabilidad de tunelización multiplicada por la frecuencia de una partícula alfa que golpea la barrera.
Téngase en cuenta que la función de onda de la partícula alfa anterior se muestra como una onda sinusoidal. Se trata con una función de onda de partículas libres, donde la amplitud de la onda representa la probabilidad y la inversa de la longitud de onda es proporcional al momento. Entonces, la función de onda trazada arriba indica que la probabilidad de encontrar la partícula alfa fuera de la barrera es mucho menor, pero si se detecta, su energía es la misma: el túnel no representa una pérdida en la energía de la partícula.
|
Índice
Referencias
Eisberg & Resnick
Sec 16-2
Rohlf
Sec 7-4
|