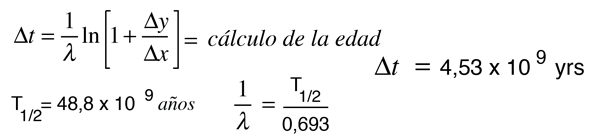Datación Radiactiva

Debido a que la semi vida radiactiva de un radioisótopo dado no se ve afectada por la temperatura, estado físico o químico, o cualquier otra influencia del medio ambiente fuera del núcleo, salvo las interacciones directas de las partículas con el núcleo, entonces, las muestras radioactivas continuan decayendo a un ritmo predecible. Es decir, cualquier núcleo radiactivo actúa como un reloj. Esto hace factible varios tipos de datación radiactiva. En la datación geológica, donde el intervalo de tiempo es del orden de la edad de la tierra y los métodos usan los relojes en las rocas, hay dos incertidumbres principales en el proceso de datación:

1. ¿Cuál fue la cantidad de elemento hijo cuando se formaron las rocas?
2. ¿Se han añadido o eliminado alguno de los átomos padre o hijo durante el proceso?

Comenzando con el caso más simple, donde no hay átomos hijo presente, y no se pierde masa de la muestra, la edad se puede determinar mediante la medición de las cantidades relativas de los isótopos. Esto se puede hacer por medios químicos, pero para las determinaciones precisas, se usa la espectrometría de masa. De las ecuaciones de desintegración radiactiva, se puede desarrollar una expresión para el tiempo transcurrido. En la práctica común nuclear de isótopos, de llamar al "padre" P y al "hijo" D, usamos estas mismas letras P y D para indicar los números correspondientes de átomos. El requisito de mantener el mismo número de núcleos da

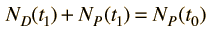
y la fórmula de decaimiento radiactivo es

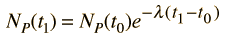
El tiempo transcurrido es entonces

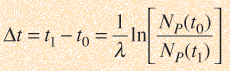
pero usando la primera expresión de arriba, se puede expresar en términos de las concentraciones presentes de los isótopos padre e hijo.

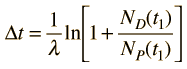
Supongamos ahora que había una cantidad original del elemento hijo presente, en el momento de formación de la muestra en estudio. Esto añade al proceso un desconocido adicional, y se necesita una pieza adicional de datos para permitir una solución del tiempo transcurrido. El requisito de las poblaciones es ahora

Afortunadamente para los procesos de datación radiactivos, la información adicional está disponible en forma de otros isótopos de elementos involucrados en el proceso radiactivo. Si hay otro isótopo del elemento hijo D', que se supone que es constante durante todo el proceso, entonces el requisito de población se puede expresar en términos de proporciones

Podemos estar razonablemente seguros de que el isótopo D' es constante si no es radiactivo (no es parte de una de las series radiactivas naturales). Utilizando la ecuación de desintegración radiactiva como anteriormente, esto se convierte en

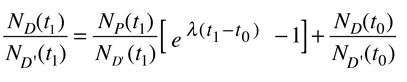
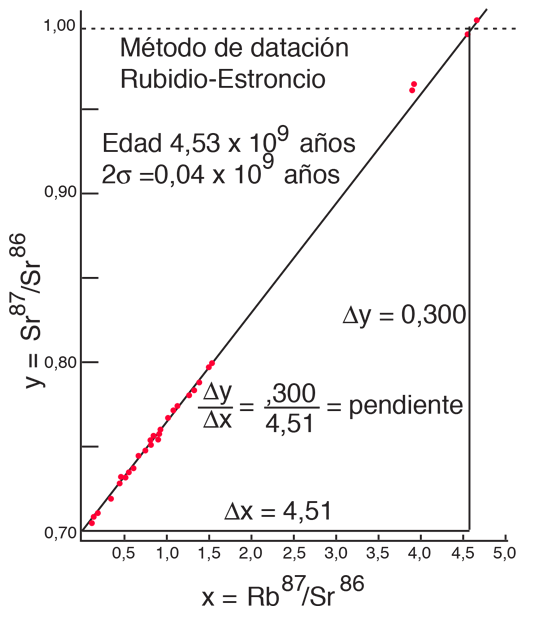
Todavía tenemos demasiadas incógnitas por resolver directamente para la edad, pero una presunción razonable es la de que todos los minerales que cristalizan juntos, deben mostrar idénticas edades e idénticas proporciones isotópicas N_D/N_D'. A continuación se puede trazar la relación y = N_D(t₁)/N_D'(t₁) contra x = N_P(t₁)/N_D'(t₁) para un número de minerales en una muestra cristalina dada, y tomar la pendiente de la línea. La edad puede ser calculada a partir de esa pendiente como sigue:

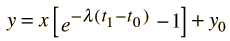Este cálculo está expresado en términos de la constante de decaimiento λ, que está relacionada con la semi vida del isótopo.

Ejemplo de Datación Rubidio/Estroncio

El cálculo de la edad en la datación geológica, debe tener en cuenta la presencia de las especies radioactivas en el comienzo del intervalo de tiempo. Si hay presente un isótopo no radiogénico del elemento hijo en el mineral, se puede utilizar como una Referencia y trazar las proporciones de los elementos padre e hijo, como proporciones con ese isótopo de referencia. La pendiente de la curva da entonces el intervalo de tiempo.