Clasificación del Espín

Un parámetro esencial para la clasificación de las partículas es su "espín" o momento angular intrínseco. Los fermiones de espín semi-entero, están limitados por el principio de exclusión de Pauli, mientras que los bosones de espín entero no lo están. El electrón es un fermión con espín electrónico de 1/2. Los quarks también son fermiones con espín 1/2. El fotón es un bosón con espín 1, que es espín típico del bosón. Las excepciones son el gravitón con espín 2 y el Bosón de Higgs con espín 0.

La clasificación del espín de las partículas, determina la naturaleza de la distribución de energía en una colección de las partículas. Las partículas de espín entero obedecen la estadísticas de Bose-Einstein, mientras que las de espín semi-entero se comportan de acuerdo con las estadísticas de Fermi-Dirac.

Carroll describe a los fermiones y los bosones de la siguiente manera: "Las partículas en el universo son de dos tipos: las partículas que forman la materia, conocidas como 'fermiones', y las partículas que llevan fuerzas, conocidas como 'bosones'. La diferencia entre las dos es que los fermiones ocupan espacio, mientras que los bosones pueden acumularse uno encima del otro. No puedes simplemente tomar un montón de fermiones idénticos y ponerlos a todos en el mismo lugar; las leyes de la mecánica cuántica no lo permitirán". El hecho de que dos fermiones idénticos no pueden ocupar el mismo estado se describe mas detalladamente en el principio de exclusión de Pauli, y el hecho de que los bosones si puedan es mejor descrito en la condensación de Bose-Einstein .

Los Fermiones

Los fermiones son partículas que tienen espín semi entero, y por lo tanto se ven limitadas por el principio de exclusión de Pauli. Las partículas con espín entero se llaman bosones. Fermiones son los electrones, los protones, y los neutrones. La función de onda que describe una colección de fermiones, debe ser antisimétrica con respecto al intercambio de partículas idénticas, mientras que la función de onda para una colección de bosones es simétrica.

El hecho de que los electrones sean fermiones, es fundamental en la construcción de la tabla periódica de los elementos, ya que sólo puede haber un electrón por cada estado en un átomo, (un solo electrón para cada conjunto posible de números cuánticos). La naturaleza fermiónica de los electrones, también regula el comportamiento de los electrones en un metal, en donde a temperaturas bajas, se llenan todos los estados de baja energía hasta un nivel llamado energía de Fermi. Este relleno de los estados, está descrito por las estadísticas de Fermi-Dirac.

Carroll analiza otro aspecto de la naturaleza de los fermiones: La materia ordinaria que incluye los elementos de la tabla periódica está compuesta de solo tres tipos de fermiones, el electrón y los quarks up y down. Son responsables de la gran diferencia de escala entre el nœcleo y el átomo. Cuánticamente, un electrón puede ser considerado como un paquete de ondas que obtiene su masa relativamente pequeña por su interacción con el campo de Higgs. La pequeña energía de masa se traduce en una característica longitud de onda relativamente larga, por lo que el paquete se extiende en el espacio. Esto le da al átomo un tamaño relativamente grande en su conjunto. Los quarks up y down que forman los protones y neutrones en el nœcleo tienen relativamente mayor masa por su interacción más fuerte con el campo de Higgs. Las longitudes de onda características de sus paquetes de ondas mecánica cuántica son mucho más pequeñas. Forman el nœcleo como una entidad mucho más pequeña que el átomo. Este enfoque de la escala del nœcleo y el átomo debería ser tomado en consideración junto con el estudio del confinamiento de partícula y el principio de incertidumbre.

Los Bosones

Los bosones son partículas que tienen espín entero, y que por lo tanto no se ven limitados por el principio de exclusión de Pauli, como los fermiones de espín semi-entero. La distribución de energía de los bosones es descrita por las estadísticas de Bose-Einstein. La función de onda que describe una colección de bosones, debe ser simétrica con respecto al intercambio de partículas idénticas, mientras que la función de onda para una colección de fermiones, es antisimétrica.

A bajas temperaturas, los bosones se comportan de manera muy diferente a los fermiones, debido a que un número ilimitado de ellos, pueden recolectarse en el mismo estado energético. La colección en un estado simple se llama condensación, o condensación de Bose-Einstein. . Es responsable del fenómeno de la superfluidez del helio líquido. Las partículas acopladas también pueden actuar eficazmente como bosones. En la teoría BCS de la superconductividad, los pares acoplados de electrones actuan como bosones, y se condensan en un estado que demuestra cero resistencia eléctrica.

Los bosones incluyen a los fotones, y la caracterización de los fotones como partículas con energía dependiente de la frecuencia, dada por la fórmula de Planck, le permitió a Planck aplicar las estadísticas de Bose-Einstein, para explicar la radiación térmica de una cavidad caliente.

En el modelo estándar de la física de partículas las partículas elementales que llevan fuerzas son bosones, como el fotón que transporta la fuerza electromagnética. Estos bosones no ocupan espacio ni constituyen objetos sólidos ya que pueden condensarse en la misma ubicación del espacio.

• Los bosones vectoriales con espín=1 son los bosones gauge del Modelo Estándar.
  • γ El fotón para la fuerza electromagnética
  • g Los ocho tipos de gluones que participan en la interacción fuerte
  • Z El bosón neutral en la interacción débil
  • W⁺ y W^- Los bosones cargados de la interacción débil
• El bosón escalar H⁰ , el bosón de Higgs con espín = 0.
• El bosón tensorial propuesto G, el gravitón con espín = 2 para la gravedad.

La Condensación de Bose-Einstein

En 1924 Einstein señaló que los bosones podrían "condensarse" en cantidades ilimitadas, en un estado fundamental único, ya que se rigen por las estadísticas de Bose-Einstein, y no están limitados por el principio de exclusión de Pauli. Se tomó poca nota de esta curiosa posibilidad, hasta que se estudió cuidadosamente el comportamiento anómalo del helio líquido a bajas temperaturas.

Cuando se enfría el helio a una temperatura crítica de 2,17 K, se produce una discontinuidad notable en la capacidad calorífica, la densidad del líquido cae, y una fracción del líquido se convierte en un "superfluido" de viscosidad cero. La superfluidez surge de la fracción de átomos de helio que se han condensado a la más baja energía posible.

El efecto de condensación también se acredita con la producción de la superconductividad. En la teoría BCS, pares de electrones están acoplados por interacciones de red, y los pares (llamados pares de Cooper) actúan como bosones, y puede condensarse en un estado de resistencia eléctrica cero.

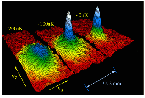
Las condiciones para el logro de un condensado Bose-Einstein son bastante extremas. Las partículas que participan deben considerarse que son idénticas, y esto es una condición que es difícil de lograr en los átomos enteros. La condición de indistinguibilidad requiere que las longitudes de onda de De Broglie de las partículas, se solapen significativamente. Esto requiere temperaturas extremadamente bajas, para que las longitudes de onda de Broglie sean largas, pero también requiere una densidad de partículas bastante alta, para reducir el hueco entre las partículas.

Desde la década de 1990 se ha producido un aumento en la investigación de la condensación de Bose-Einstein, ya que se descubrió que los condensados de Bose-Einstein, podrían estar formados por átomos ultra-fríos. El uso del enfriamiento por láser y las capturas de átomos ultra-fríos con trampas magnéticas, han producido temperaturas en el rango de nanokelvin. Cornell y Wieman junto con Ketterle del MIT recibió el Premio Nobel 2001 de Física "por el logro del condensado de Bose-Einstein en gases diluidos de átomos alcalinos, y por los primeros estudios fundamentales de las propiedades de los condensados". Cornell y Wieman encabezaron un grupo activo en la Universidad de Colorado. Boulder ha producido condensados de Bose-Einstein con átomos de rubidio. Otros grupos en el MIT, Harvard y Rice, han estado muy activos en este campo que avanza rápidamente.