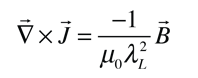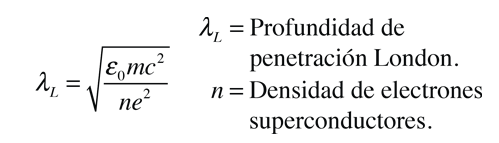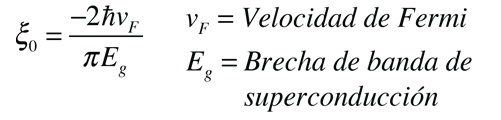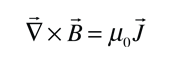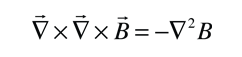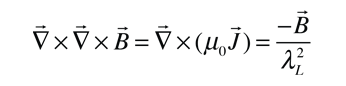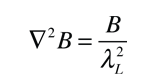Longitudes Características en los Superconductores

Con origen en las investigaciones teóricas y experimentales de la superconductividad, existen dos longitudes características, la longitud de penetración de London y la longitud de coherencia.

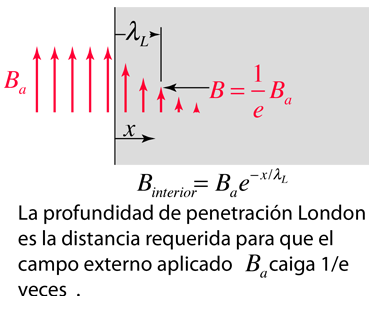
La longitud de penetración de London, se refiere al campo magnético que decae de manera exponencial en la superficie de un superconductor. Se relaciona con la densidad de los electrones de superconducción en el material. Al hecho de la exclusión de los campos magnéticos del interior del superconductor, se denomina efecto Meissner.

Una longitud característica independiente, es la llamada longitud de coherencia. Se relaciona con la velocidad de Fermi para el material y la banda de energía prohibida, asociada con la condensación del estado superconductor. Esto tiene que ver con el hecho de que la densidad de electrones superconductores no puede cambiar rápidamente. Hay una longitud mínima sobre la cual se puede realizar un cambio, sin destruir el estado superconductor. Por ejemplo, una transición desde el estado superconductor a un estado normal, tendrá una capa de transición de espesor finito, que está relacionada con la longitud de coherencia. Los estudios experimentales de varios superconductores, han dado lugar a los siguientes valores calculados para estos dos tipos de longitudes características.

Longitud de Penetración London en los Superconductores

La ecuación London es uno de los enfoques teóricos para describir el estado de superconducción. Relaciona el rotacional de la densidad de corriente J, con el campo magnético:

La ecuación London requiere que el campo magnético decaiga exponencialmente a cero dentro del conductor (ver estudio del efecto Meissner). La naturaleza del decaimiento (ver capítulo 12 de Kittel) depende de la densidad de electrones de superconducción n:

Longitud de Coherecia en los Superconductores

Una de las longitudes características para la descripción de los superconductores se llama longitud de coherencia. Se relaciona con la velocidad Fermi del material, y la banda de energía prohibida, asociada con la condensación al estado de superconducción. Esto tiene que ver con el hecho de que la densidad de electrones superconductores no puede cambiar rápidamente. Hay una longitud mínima sobre la cual se puede realizar un cambio, sin destruir el estado superconductor. Por ejemplo, una transición desde el estado superconductor a un estado normal, tendrá una capa de transición de espesor finito, que está relacionada con la longitud de coherencia.

Efecto Meissner por la Ecuación London

La ecuación London relaciona el rotacional de la densidad de corriente J con el campo magnético:

Relacionando la ecuación de London con las ecuaciones de Maxwell, se puede demostrar que el efecto Meissner, surge de la ecuación de London. Una de las ecuaciones de Maxwell es

Usando la identidad de cálculo vectorial

junto con el rotacional de la ecuación de Maxwell de arriba

y por sustitución

Como