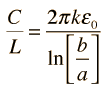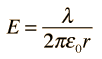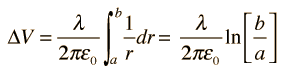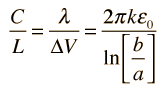
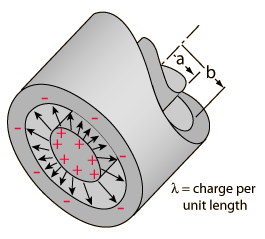
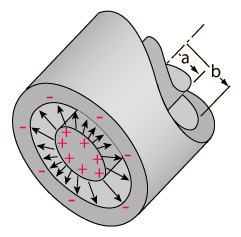
Condensador Cilíndrico

En una geometría cilíndrica como un cable coaxial, la capacidad se suele establecer como capacidad por unidad de longitud. Las cargas eléctricas se encuentran en la superficie exterior del conductor interior y en la pared interna del conductor exterior. La expresión para la capacidad es

Mostrar

Para un radio interior a = m,
radio exterior b = m ,
y constante dieléctrica k = ,
la capacidad por unidad de longitud es
C/L = F/m = x10^ F/m = pF/m
Para una longitud de L = m la capacidad es
C = F = x10^ F = pF

Índice

Conceptos sobre Condensador
 
HyperPhysics*****Electricidad y MagnetismoM Olmo R Nave
 Atrás






Condensador Cilíndrico

La capacidad de los conductores cilíndricos o esféricos se puede obtener evaluando la diferencia de voltaje entre los conductores, para una determinada carga en cada uno. Aplicando la ley de Gauss a un cilindro infinito en el vacío, el campo eléctrico exterior de un cilindro cargado se da por

El voltaje entre cilindros se puede encontrar integrando el campo eléctrico a lo largo de una línea radial:

De la definición de capacidad e incluyendo el caso donde el volumen se rellena con un dieléctrico de constante dieléctrica k, la capacidad por unidad de longitud se define como
Cálculo
 Índice

Conceptos sobre Condensador
 
HyperPhysics*****Electricidad y MagnetismoM Olmo R Nave
 Atrás