Cálculo: Máximo y Mínimo
La determinación de los valores máximos y mínimos de una función, es uno de los logros de la gran potencia que tiene el Cálculo. Tomemos f(x) como una función de x. El valor de x para el cual la derivada de f(x) con respecto a x es igual a cero, corresponden a los puntos de inflexión de la función f(x) donde sus valores son máximo y mínimo.
Por ejemplo, la altura de un proyectil que se dispara en línea recta, está dada por las ecuaciones del movimiento:
Abajo se muestra la gráfica de la altura y(t), tomando y0 = 0.
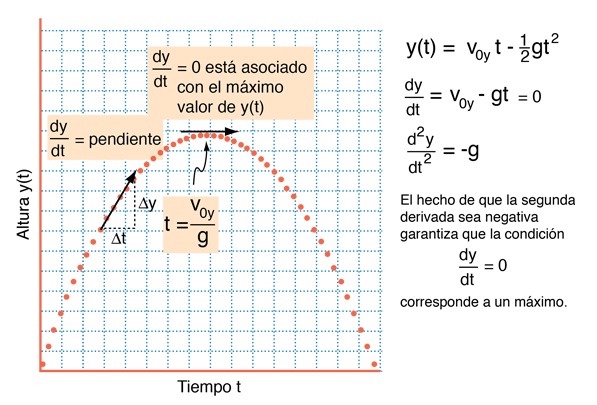
La derivada de una función puede ser interpretada geométricamente como la pendiente de la curva de la función matemática y(t), representada la derivada en función de t. La derivada es positiva cuando una función es creciente hacia un máximo, cero (horizontal) en el máximo, y negativa justo después del máximo. La segunda derivada es la tasa de cambio de la primera derivada y es negativa en el proceso que se acaba de describir, puesto que la primera derivada (la pendiente), siempre es cada vez mas pequeña. La segunda derivada es siempre negativa en la "joroba" de una función, que corresponde a un máximo de la función.
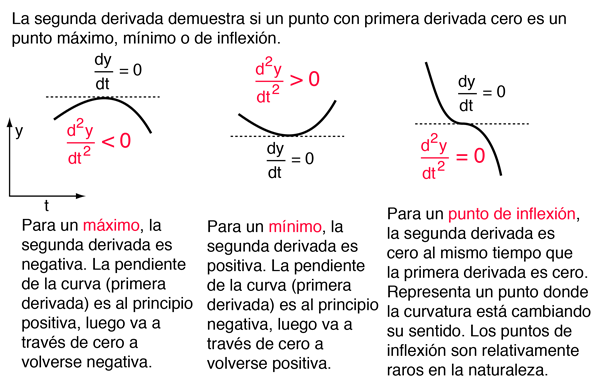
En la función simple que se ha mostrado en el ejemplo solo hay un máximo. Las funciones mas complejas pueden tener múltiples máximos y mínimos y la segunda derivada, nos proporciona la manera de distinguirlos.
| Ejemplos de problemas de máximos y mínimos | Principio de Fermat |
| Mínima Energía. Oscilador Armónico | |
| Máxima Probabilidad. Radio del Hidrógeno |
Conceptos de Derivada
Conceptos de Integral
| HyperPhysics*****HyperMath*****Cálculo | M Olmo R Nave |