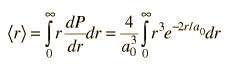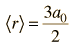Radio Mas Probable
Estado Fundamental del Hidrógeno
 |
La densidad de probabilidad radial del estado fundamental del hidrógeno, se obtiene multiplicando el cuadrado de la función de onda por un elemento de volumen de capa esférica. 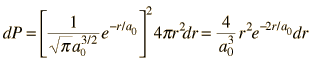 Toma esta forma comparativamente simple, porque el estado 1s es esféricamente simétrico, y no aparecen términos angulares. |
Dejando los términos constantes, tomando la derivada con respecto a r, y estableciendola igual a cero, da el radio de máxima probabilidad.
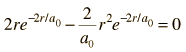
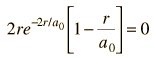
el cual da
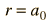
donde
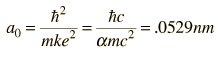
El radio mas probable, es el radio del estado fundamental obtenido de la teoría de Bohr. La ecuación de Schrodinger confirma el primer radio de Bohr, como el radio mas probable, pero va mas alla y describe en detalle, el perfil de probabilidad para el radio del electrón.
| Probabilidad del Rango del Radio |
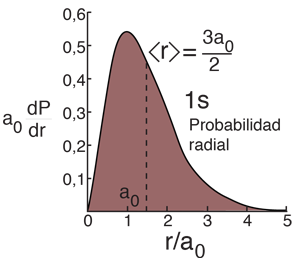
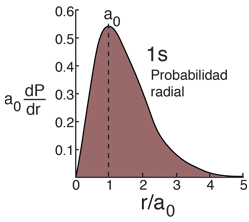
| Valor Esperado del Radio |
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
| HyperPhysics*****Física Cuántica | M Olmo R Nave |