Maxima and Minima from Calculus
One of the great powers of calculus is in the determination of the maximum or minimum value of a function. Take f(x) to be a function of x. Then the value of x for which the derivative of f(x) with respect to x is equal to zero corresponds to a maximum, a minimum or an inflexion point of the function f(x).
For example, the height of a projectile that is fired straight up is given by the motion equations:
Taking y0 = 0, a graph of the height y(t) is shown below.
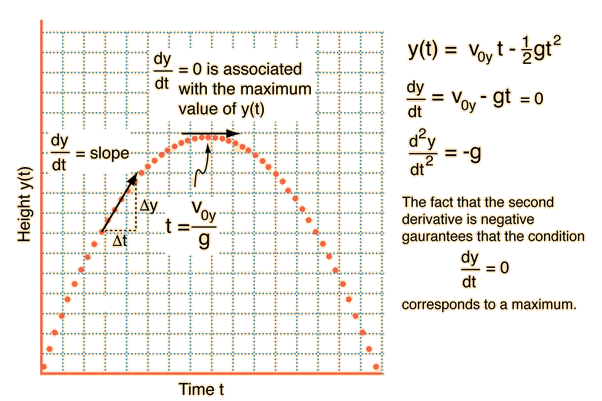
The derivative of a function can be geometrically interpreted as the slope of the curve of the mathematical function y(t) plotted as a function of t. The derivative is positive when a function is increasing toward a maximum, zero (horizontal) at the maximum, and negative just after the maximum. The second derivative is the rate of change of the derivative, and it is negative for the process described above since the first derivative (slope) is always getting smaller. The second derivative is always negative for a "hump" in the function, corresponding to a maximum.

For the simple function used in the example, there is only one maximum. More complex functions can have multiple maxima and minima, and the evaluation of the second derivative provides a way to distinguish them.
| Examples of maximum-minimum problems | Fermat's principle |
| Minimum energy, harmonic oscillator | |
| Maximum probability, hydrogen radius | |
| Minimize chromatic aberration |
Derivative concepts
Integral concepts
| HyperPhysics*****HyperMath*****Calculus | R Nave |