Image from System Matrix

The position of the image formed by a thick lens can be found by using the system matrix. This involves multiplying a vector form of the incident vergence successively by three matrices representing (1)the refraction by the first surface, (2)the translation to the second surface, and (3) the refraction by the second surface. Those three operations can be combined to form the system matrix. The entrance vergence can then be just multiplied times the system matrix to determine the exit vergence and from that vergence, the image distance is calculated.

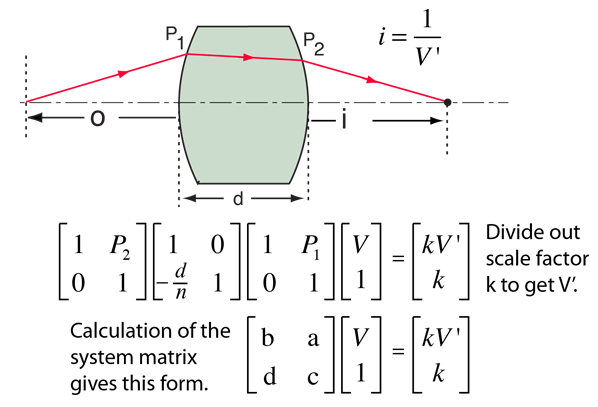
The example is for a lens with index of refraction n surrounded by air (n=1). It involves the surface powers of the lens and the thickness d between the vertexes. It also involves the principal planes H₁ and H₂. As with most ordinary geometrical optics, it is applicable only for small angles (paraxial rays). The development also follows the cartesian sign convention.

For glass with index of refraction nlens = n = the front surface power for lens radius R1 = m is P1 = m-1 and the back surface power for lens radius R2 = m is P2 = m-1 Lens thickness d = m (Note that for a double convex lens, the front surface radius R1 is positive and the back surface radius R2 is negative according to the Cartesian sign convention.)

The symbols used by Meyer-Arendt for the elements of the system matrix will be used. b = a = d = c =

**********

A number of other characteristics of the thick lens may be calculated from the system matrix.

The right-hand, or equivalent focal length of the lens is just the reciprocal of matrix element a: f₂ = 1/a = m.

The distance V₂H₂ from the right vertex to the associated principal plane is given by V₂H₂= (c-1)/a = m.

The right vertex focal length (or back focal length) is given by f_v2 = c/a = m.

Note that the equivalent focal length f₂ is the sum of the back vertex focal length and the distance from the vertex to the principal plane: f₂ = f_v2 + V₂H₂. Similar relationships exist for the left-hand or front vertex.

The left vertex focal length (or front focal length) is given by f_v1 = -b/a = m.

The distance V₁H₁ from the left vertex to the associated principal plane is given by V₁H₁= (1-b)/a = m.

The equivalent front focal length f₁ is then given by f₁ = -(b/a + V₁H₁) = m. **********

For object* distance o = m, the value of the input vergence V = . Performing the indicated matrix multiplication at left gives: kV'= k=. Dividing both by k gives the exit vergence V' = m-1 so the image distance i = m

*Using the Cartesian sign convention, the object distance is typically a negative number since it points opposite to the direction of light travel. The input vergence is therefore negative (divergent).

The equivalent power for the thick lens can be calculated from Gullstrand's equation:

Note that the calculation does not take into account the change in lens thickness with the angle of the incoming ray. It is typical to do the calculation only for the paraxial rays where the departure from full thickness is negligible.