A Good Absorber is a Good Emitter
According to the Stefan-Boltzmann law, the energy radiated by a blackbody radiator per second per unit area is proportional to the fourth power of the absolute temperature and is given by
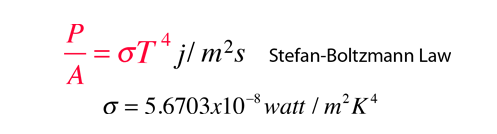
For hot objects other than ideal radiators, the law is expressed in the form:
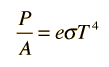
where e is the emissivity of the object (e = 1 for ideal radiator). If the hot object is radiating energy to its cooler surroundings at temperature Tc, the net radiation loss rate takes the form
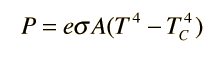
In this relationship the term with Tc represents the energy absorbed from the environment. This expression explicitly assumes that the same coefficient e applies to both the emission into the environment and the absorption from the environment. That is, a good emitter is a good absorber and vice versa; the same coefficient can be used to characterize both processes. Why is that true?
Perhaps the most fundamental conceptual way to approach this question is to observe that a hot object placed in a room must ultimately come to thermal equilibrium with the room. The hot object will initially emit more energy into the room than it absorbs from the room, but that will cause the temperature of the room to rise and the temperature of the object to drop. But when they reach the same temperature, we can conclude that the amount of energy absorbed on average is exactly the same as the energy emitted. That is, the expression above for net energy radiated to the environment must give us zero when T=Tc.
The above argument is based upon the Second Law of Thermodynamics in the form that states that heat will not spontaneously flow from a cold object to a hot object. If the absorption coefficient were higher than the emission coefficient for the object, then it could absorb net energy from the room even when its temperature were higher than the room.
But suppose you wanted to argue that a good absorber must be a good emitter based on the microscopic processes involving the atoms in the surface of an object. Then it becomes quantum question and involves the following ideas:
1. All electromagnetic radiation can be considered to be quantized, existing as photons with energy given by the Planck hypothesis, E=hf.
2. In order for a solid (or any matter, but I am assuming we are talking about solids) to absorb a photon of given energy hf , it must have a pair of energy levels separated by that amount of energy hf, so that the photon elevates the system from the lower member of the pair to the upper.
3. For visible light or near visible, then energy level pairs involved in most absorption are electron energy levels, so that when you absorb a green photon of photon energy 2.2 eV, you are causing an electron very near the surface of the solid to jump upward 2.2 eV. It can't do it unless there is a level at 2.2 eV up to receive it.
4. If a surface is an ideal absorber in the visible, this implies that there is an abundance of available electron states so that a photon of any color in the visible spectrum can interact with electrons in the solid to elevate them to an available upper level. The implication is that any color in the visible spectrum can be readily absorbed, hence it is an ideal absorber, a perfectly black object.
5. The next step is not so obvious. If a pair of electron energy levels is available for absorption of a photon, it is also available for emission of a photon, i.e. , radiation. If it is available for an upward jump, it is available for a downward jump. One of Einstein's contributions was to show that for a given radiation, the probability for emission is the same as the probability of absorption. This fact is described in terms of the Einstein A and B coefficients and is very important in laser theory. The implication for the current question is that it constrains a good absorber to also be a good emitter. If the solid has lots of available electron levels for absorption, they will also be equally available for emission. To bring the discussion full circle, Einstein first derived his A and B coefficients from a thermodynamic argument like the argument above about thermal equilibrium before the actual development of the quantum mechanical ideas.
The bottom line of this reasoning is that a good absorber of radiation will also be a good emitter. But the above is just the tip of the iceberg. For a black object, all visible colors are absorbed by electron jumps, but the elevated electrons usually follow a different path downward, cascading down in smaller jumps associated with perhaps infrared radiation. So we say that the light is absorbed and heats the object, associating heat with the infrared range of the electromagnetic spectrum. Nevertheless, it is a good emitter, just taking the light in as visible and reradiating it as infrared. For such a radiator at equilibrium, the fraction of light it emits in any wavelength range depends upon the temperature and for the ideal radiator is distributed in wavelength according to the blackbody relationship. The great complexity of dealing with all the quantum mechanisms and processes in a solid is the kind of thing that might have led Einstein to his purported preference for approaching problems from a thermodynamic perspective whenever possible.
Blackbody radiation concepts
Heat transfer concepts
| HyperPhysics***** Thermodynamics ***** Quantum Physics | R Nave |