Multiplicidad en la Distribución de Energía
La evaluación del número de maneras en que podemos distribuir la energía entre una colección de partículas o sistemas, es importante en el cálculo físico, puesto que cualquier colección tenderá hacia la configuración de máxima multiplicidad (máxima entropía).
La multiplicidad Ω de q unidades de energía entre N estados igualmente probables, está dada por la expresión:
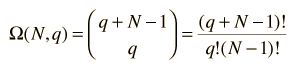
A esto a veces se le denomina como número de microestados del sistema.
Shroeder tiene una manera sucinta de demostrar la fórmula de arriba. Supongamos que usamos un punto para representar cada una de las unidades de energía q, y una línea vertical para representar los límites entre los N estados. Un ejemplo de la distribución de q=8 unidades de energía en N=4 estados, podría ser
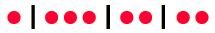
Ahora esto se puede ver como una distribución de dos tipos de elementos: unidades de energía (puntos) y límtes entre estados (líneas verticales). Siempre habrá q unidades de energía y N-1 límites entre estados, con un total de q+N-1 símbolos (11 en este ejemplo). De modo que el número de formas de distribuir q unidades de energía, debería ser exactamente la siguiente combinación
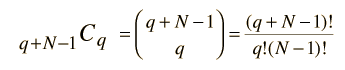
que es el número de maneras de escoger q unidades de energía (la permutación) dividido por el número de formas diferentes de reagrupar las q unidades sin cambiar el número de ellas en cada estado.
Conceptos de Estadística Aplicada
Referencia
Schroeder Sec. 2.2
| HyperPhysics*****HyperMath*****Álgebra | M Olmo R Nave |