Entropía y el Gas Ideal
La entropía S de un gas ideal monoatómico, se puede expresar en una famosa ecuación llamada la ecuación de Sackur-Tetrode.
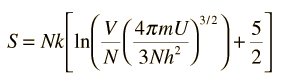
donde
- N = número de átomos
- k = constante de Boltzmann
- V = volumen
- U = energía interna
- h = constante de Planck
Una de las cosas que se pueden determinar directamente de esta ecuación, es el cambio en la entropía durante una expansión isotérmica, donde N y U son constantes (implicando Q=W). Expandiendo la expresión de la entropía para Vf y Vi, y con la regla de combinación de logaritmos nos lleva a
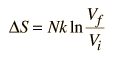
Para determinar otras funciones, es útil expandir la expresión de la entropía para separar la dependencia de U y V.
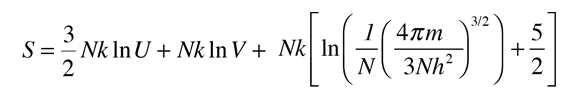
Luego, usando la definición de temperatura en términos de la entropía:
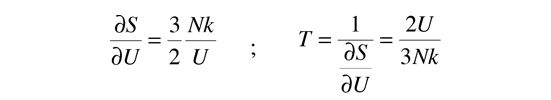
Esto da una expresión para la energía interna que es consistente con la equipartición de energía.
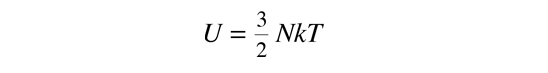
con kT/2 de energía para cada grado de libertad de cada átomo.
En el proceso con un gas ideal, se puede calcular el cambio en la entropía de la relación

Haciendo uso de la primera ley de la termodinámica y la naturaleza del trabajo del sistema, esto se puede escribir
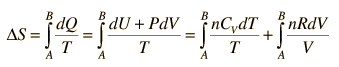
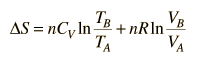 |
|
Esta es una fórmula de cálculo útil si se conocen la temperatura y el volumen, pero si trabajamos en un diagrama PV, es preferible tenerlo expresado en estos términos. Usando la ley de gas ideal
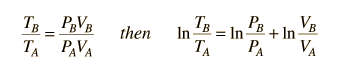
luego
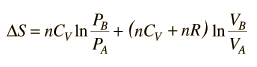 .
.Pero como los calores específicos están relacionados por CP = CV + R,
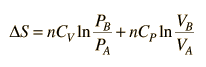 .
.Como la entropía es una variable de estado, dependiente solamente de los estados inicial y final, se pueden usar estas expresiones para cualquiera de dos puntos que se pueda poner en uno de los gráficos estándares.
Conceptos sobre Entropía
Referencia
Schroeder
Cap. 2
| HyperPhysics*****Termodinámica | M Olmo R Nave |