Einstein Model of a Solid

A useful step on the way to understanding the specific heats of solids was Einstein's proposal in 1907 that a solid could be considered to be a large number of identical oscillators. The quantum approach to the harmonic oscillator gives a series of equally spaced quantized states for each oscillator, the separation being hf where h is Planck's constant and f is the frequency of the oscillator. The sketch below visualizes a group of uniformly spaced oscillators in a solid, with any interaction between them neglected for the present.

The conceptual Einstein solid is useful for examining the idea of multiplicity in the distribution of energy among the available energy states of the system. All of the energy levels are considered to be equally probable within the constraint of having q units of energy and N oscillators.

As an example, consider q=3 units of energy distributed in an Einstein solid with N=4 oscillators.

At left is the detailed listing of the possible distributions of the energy, a total of 20 different distributions for 3 units of energy among 4 oscillators (a multiplicity of 20). If we are trying to develop a description of a real solid with Avogadro's number of oscillators, this kind of approach is clearly impractical. Fortunately, mathematical expressions for the multiplicity make the task manageable. The multiplicity for q units of energy among N oscillators is given by the expression: which for this example becomes 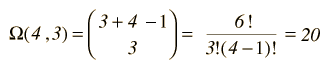More details about the multiplicity expression.

The entropy of the Einstein solid can be expressed in terms of the multiplicity.

To make the multiplicity expression manageable, consider the following steps:

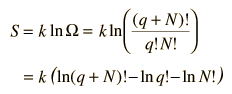
The numbers q and N are presumed large and the 1 is dropped. Now making use of Stirling's approximation to evaluate the factorials

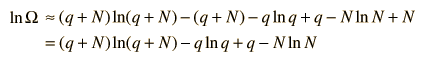
Now making the physical assumption that the number of energy units is much larger than the number of oscillators, q>>N, the expression can be further simplified. With rearrangement

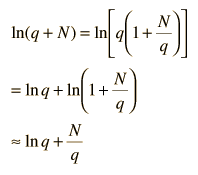
Besides making use of log combination rules, the above steps make use of the series expansion of ln(1+N/q) which can be approximated by the first term when q>>N: (approximately, ln(1+x)=x if x<<1). Substitution gives an expression for the entropy of the Einstein solid:

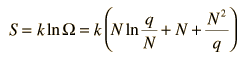
Finally we can make a connection to something akin to a real-world solid. The internal energy U can be represented by q times the oscillator energy unit hf = ε. The last term above will be negligible under the assumption q>>N, so the entropy expression becomes

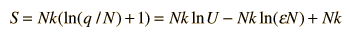
Using the definition of temperature as a function of entropy gives

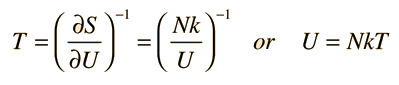
This is what is expected from equipartition of energy. Each oscillator has two degrees of freedom, and each should represent kT/2 of energy, giving U=NkT.