Matriz del Sistema: Dos Lentes Finas

La posición de la imagen formada por un par de lentes delgadas se puede encontrar por el método de la matriz. El método general de la matriz implica multiplicar una forma vectorial de la vergencia incidente sucesivamente por matrices que representan (1) la refracción por la primera lente, (2) la translación a la segunda lente, y (3) la refracción por la segunda lente. Si se calcula la matriz del sistema se puede utilizar para multiplicar directamente la vergencia incidente para obtener la vergencia de salida. A partir de esa vergencia de salida se calcula la distancia de la imagen.

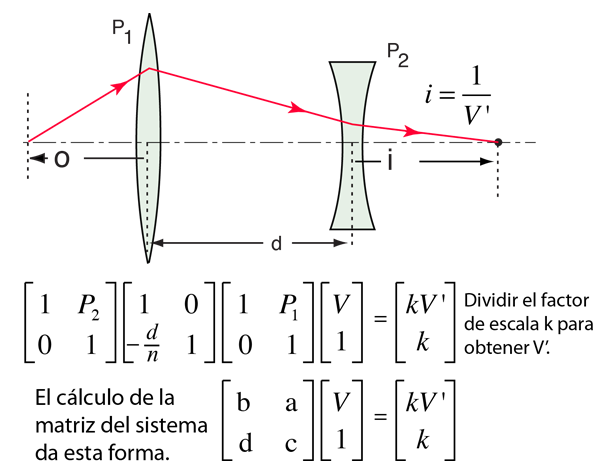
Este ejemplo es para dos lentes delgadas rodeadas por aire (n = 1). Implica a las potencias de las lentes y la separación d de las lentes. También implica los planos principales H₁ y H₂. Como con la mayoría de las ópticas geométricas ordinarias, es aplicable solo para ángulos pequeños (rayos paraxiales). El desarrollo también sigue la convención de signos cartesianos.

Se proporciona un conjunto predeterminado de valores para los parámetros de este cálculo. Puede ver el cálculo predeterminado ingresando un 0 en uno de los parámetros de la lente, lo que activará la entrada de los parámetros predeterminados para las lentes. Cualquiera de ellos puede cambiarse para explorar el comportamiento del sistema de lentes.

La potencia para la lente 1 es P₁ = m^-1

La potencia para la lente 2 es P₂ = m^-1

La separación de lentes d = m

Se utilizarán los símbolos utilizados por Meyer-Arendt para los elementos de la matriz del sistema. b = a = d = c =

****************

A partir de la matriz del sistema se puede calcular una serie de otras características de la lente delgada.

La mano derecha, o la distancia focal equivalente de la lente es justo el recíproco del elemento de matriz a: f₂ = 1/a = m.

La distancia V₂H₂ desde el vértice derecho al plano principal asociado está dado por V₂H₂= (c-1)/a = m.

La longitud focal del vértice derecho (o longitud focal posterior) está dada por f_v2 = c/a = m.

Nótese que la longitud focal equivalente f₂ es la suma de la longitud focal del vértice posterior y la distancia desde el vértice al plano principal: f₂ = f_v2 + V₂H₂. Existen relaciones similares para el vértice izquierdo o frontal.

La longitud focal del vértice izquierdo (o longitud focal frontal) está dada por f_v1 = -b/a = m.

La distancia V₁H₁ desde el vértice izquierdo al plano principal asociado está dada por V₁H₁= (1-b)/a = m.

La longitud focal frontal equivalente f₁ está dada por f₁ = -(b/a + V₁H₁) = m.
****************************

Localización de la Imagen con la Matriz del Sistema

Recordatorio: Usando la convención de signos cartesianos, la distancia del objeto suele ser un número negativo, ya que apunta en dirección opuesta a la dirección de la luz.

Para una distancia de objeto* o = m, el valor de la vergencia de entrada V = . Realizando la multiplicación de matriz indicada da: kV'= k=. Dividiendo ambos por k da la vergencia de salida V' = m-1 de modo que la distancia de la imagen i = m.

Nótese que el cálculo no tiene en cuenta el cambio en la separación de la lente con el ángulo del rayo de entrada. Es típico hacer el cálculo solamente para los rayos paraxiales donde la desviación de la separación total es despreciable.